0 136594 136602 136608 136612 136618 136620 136624 136630 136632 136638 136644 136648 136650 136654 136660 136662 136668 136672 136674 136678 136680 136684 136686 136688 136689 136690 136692 136693 136694 136696 136698 136702 136704 136708 136710 136714 136720 136722 136728 136732 136734 136738 136744 136750 136752 136758 136762 136764 136770 136774 136780 136788 447348
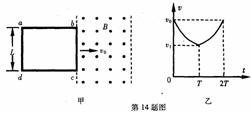 (1)求t=0时刻线圈的电功率;
(1)求t=0时刻线圈的电功率;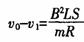
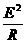 =
=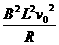
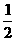 mv02-
mv02-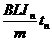
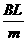 (I1L1+I2L2+…+InLn)
(I1L1+I2L2+…+InLn)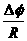 =
=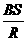
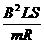
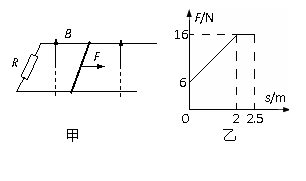 (2)拉力F作用过程中,电阻R上产生的焦耳热;
(2)拉力F作用过程中,电阻R上产生的焦耳热;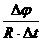 =BLs΄/(RΔt)
=BLs΄/(RΔt)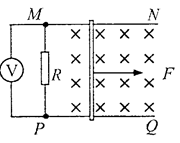 如图所示,光滑且足够长的平行金属导轨
如图所示,光滑且足够长的平行金属导轨 和
和 固定在同一水平面上,两导轨间距,电阻
固定在同一水平面上,两导轨间距,电阻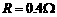 ,导轨上静止放置一质量
,导轨上静止放置一质量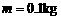 、电阻
、电阻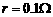 的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度
的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度 的匀强磁场中,磁场的方向竖直向下,现用一外力
的匀强磁场中,磁场的方向竖直向下,现用一外力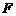 沿水平方向拉杆,使之由静止起做匀加速运动并开始计时,若5s末理想电压表的读数为0.2V.求:
沿水平方向拉杆,使之由静止起做匀加速运动并开始计时,若5s末理想电压表的读数为0.2V.求: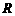 上消耗的电功率;
上消耗的电功率;
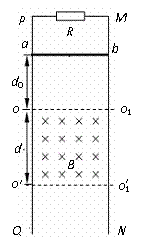 如图,竖直放置的光滑平行金属导轨MN、PQ相距L,在M点和P点间接一个阻值为R的电阻,在两导轨间 OO1O1′O′ 矩形区域内有垂直导轨平面向里、宽为d的匀强磁场,磁感应强度为B.一质量为m,电阻为r的导体棒ab垂直搁在导轨上,与磁场上边边界相距d0.现使ab棒由静止开始释放,棒ab在离开磁场前已经做匀速直线运动(棒ab与导轨始终保持良好的电接触且下落过程中始终保持水平,导轨电阻不计).求:
如图,竖直放置的光滑平行金属导轨MN、PQ相距L,在M点和P点间接一个阻值为R的电阻,在两导轨间 OO1O1′O′ 矩形区域内有垂直导轨平面向里、宽为d的匀强磁场,磁感应强度为B.一质量为m,电阻为r的导体棒ab垂直搁在导轨上,与磁场上边边界相距d0.现使ab棒由静止开始释放,棒ab在离开磁场前已经做匀速直线运动(棒ab与导轨始终保持良好的电接触且下落过程中始终保持水平,导轨电阻不计).求: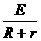 …………………………(1分)
…………………………(1分)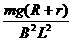 ……………………………(1分)
……………………………(1分) ……………………(1分)
……………………(1分)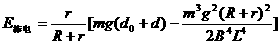 ……………………(1分)
……………………(1分) …(1分)
…(1分)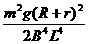 时,棒进入磁场后做匀速直线运 ………(1分)
时,棒进入磁场后做匀速直线运 ………(1分)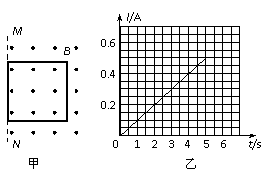
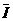 t,由I-t图象得:q =1.25C (2分)
t,由I-t图象得:q =1.25C (2分) =
=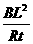 (2分)
(2分)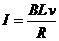 ,可得金属框的速度随时间也是线性变化的,
,可得金属框的速度随时间也是线性变化的,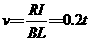 (1分)
(1分)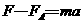 (1分)
(1分)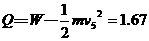 J (3分)
J (3分)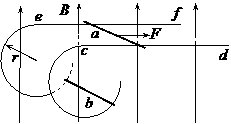 如图所示,足够长的光滑平行金属导轨cd和ef,水平放置且相距L,在其左端各固定一个半径为r的四分之三金属光滑圆环,两圆环面平行且竖直。在水平导轨和圆环上各有一根与导轨垂直的金属杆,两金属杆与水平导轨、金属圆环形成闭合回路,两金属杆质量均为m,电阻均为R,其余电阻不计。整个装置放在磁感应强度大小为B、方向竖直向上的匀强磁场中。当用水平向右的恒力F=
如图所示,足够长的光滑平行金属导轨cd和ef,水平放置且相距L,在其左端各固定一个半径为r的四分之三金属光滑圆环,两圆环面平行且竖直。在水平导轨和圆环上各有一根与导轨垂直的金属杆,两金属杆与水平导轨、金属圆环形成闭合回路,两金属杆质量均为m,电阻均为R,其余电阻不计。整个装置放在磁感应强度大小为B、方向竖直向上的匀强磁场中。当用水平向右的恒力F=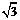 mg拉细杆a,达到匀速运动时,杆b恰好静止在圆环上某处,试求:
mg拉细杆a,达到匀速运动时,杆b恰好静止在圆环上某处,试求: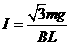 (2分)
(2分)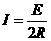
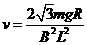 (4分)
(4分)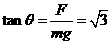 得:θ=60°
得:θ=60°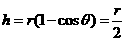 (4分)
(4分)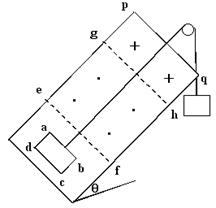 (1)求ef线和gh线间的距离;
(1)求ef线和gh线间的距离;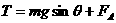 (1分)
(1分)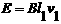
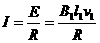 受到的安培力
受到的安培力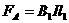 (1分)
(1分)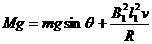
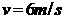 (2分)
(2分)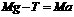 对m:
对m: 
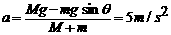 (1分)
(1分)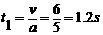
 (1分)
(1分)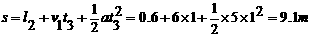 (1分)
(1分)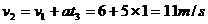
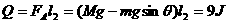 (3分)
(3分) (2分)
(2分)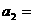
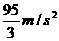
 过程中,整个回路中产生的焦耳热.
过程中,整个回路中产生的焦耳热.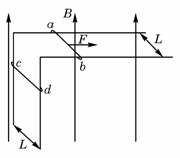
 (1分)
(1分) ① (2分)
① (2分)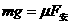 ②
(2分)
②
(2分)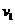 =
=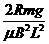 ③
(1分)
③
(1分)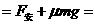
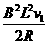 +μmg
+μmg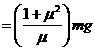 ④ (3分)
④ (3分)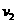 速度向下运动
速度向下运动 距离,
距离,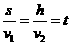 , ∴
, ∴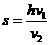 (2分)
(2分)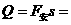
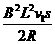 =
=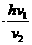 =
=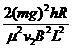 (2分)
(2分) 和匀强磁场的宽度d。
和匀强磁场的宽度d。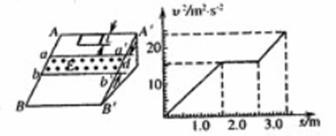
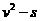 图象可知,金属框从开始运动到位移
图象可知,金属框从开始运动到位移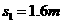 过程中,做匀加速直线运动。根据运动学公式
过程中,做匀加速直线运动。根据运动学公式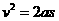 ①,动力学公式
①,动力学公式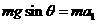 ②,代入数据解得
②,代入数据解得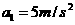 ,
,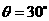 。
。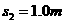 ,加速度
,加速度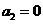 ,速度
,速度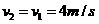 ;从2.6m运动到3.4m过程中做匀加速直线运动,
;从2.6m运动到3.4m过程中做匀加速直线运动,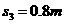 ,初速度
,初速度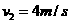 ,加速度
,加速度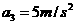 。由此可判断,金属框从进入磁场开始到完全离开磁场一直在做匀速直线运动,故s2=2d③,d=0.5 m。
。由此可判断,金属框从进入磁场开始到完全离开磁场一直在做匀速直线运动,故s2=2d③,d=0.5 m。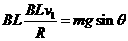 ④,解得
④,解得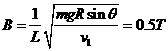 。
。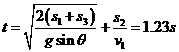 ⑤
⑤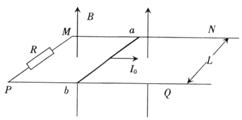 如图所示,足够长的金属导轨MN和PQ与R相连,平行地放在水平桌面上,质量为m的金属杆可以无摩擦地沿导轨运动.导轨与ab杆的电阻不计,导轨宽度为L,磁感应强度为B的匀强磁场垂直穿过整个导轨平面.现给金属杆ab一个瞬时冲量I0,使ab杆向右滑行.
如图所示,足够长的金属导轨MN和PQ与R相连,平行地放在水平桌面上,质量为m的金属杆可以无摩擦地沿导轨运动.导轨与ab杆的电阻不计,导轨宽度为L,磁感应强度为B的匀强磁场垂直穿过整个导轨平面.现给金属杆ab一个瞬时冲量I0,使ab杆向右滑行.