0 136593 136601 136607 136611 136617 136619 136623 136629 136631 136637 136643 136647 136649 136653 136659 136661 136667 136671 136673 136677 136679 136683 136685 136687 136688 136689 136691 136692 136693 136695 136697 136701 136703 136707 136709 136713 136719 136721 136727 136731 136733 136737 136743 136749 136751 136757 136761 136763 136769 136773 136779 136787 447348
 宽L=0.2m,轨道平面内有竖直向上的匀强磁场, 磁感应强度B=0.5T,ab和cd棒均静止在导轨上,质量相等为m=0.1kg,电阻相等为R=0.5Ω.现用F=0.2N向右的水平恒力使ab棒由静止开始运动,经t=5s,ab棒的加速度a=1.37m/s2,则:
宽L=0.2m,轨道平面内有竖直向上的匀强磁场, 磁感应强度B=0.5T,ab和cd棒均静止在导轨上,质量相等为m=0.1kg,电阻相等为R=0.5Ω.现用F=0.2N向右的水平恒力使ab棒由静止开始运动,经t=5s,ab棒的加速度a=1.37m/s2,则: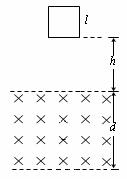 如图所示,水平的平行虚线间距为d=50cm,其间有B=1.0T的匀强磁场。一个正方形线圈边长为l=10cm,线圈质量m=100g,电阻为R=0.20Ω。开始时,线圈的下边缘到磁场上边缘的距离为h=80cm。将线圈由静止释放,其下边缘刚进入磁场和刚穿出磁场时的速度相等。取g=10m/s2,
如图所示,水平的平行虚线间距为d=50cm,其间有B=1.0T的匀强磁场。一个正方形线圈边长为l=10cm,线圈质量m=100g,电阻为R=0.20Ω。开始时,线圈的下边缘到磁场上边缘的距离为h=80cm。将线圈由静止释放,其下边缘刚进入磁场和刚穿出磁场时的速度相等。取g=10m/s2,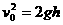 (1分)
(1分) E=BLV (1分)
E=BLV (1分)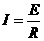 (1分)
(1分)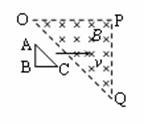 如图所示,等腰直角三角形OPQ区域内存在匀强磁场,另有一等腰直角三角形导线框ABC以恒定的速度沿垂直于磁场方向穿过磁场,穿越过程中速度始终与AB边垂直且保持AC平行于OQ。关于线框中的感应电流,以下说法中正确的是BC
如图所示,等腰直角三角形OPQ区域内存在匀强磁场,另有一等腰直角三角形导线框ABC以恒定的速度沿垂直于磁场方向穿过磁场,穿越过程中速度始终与AB边垂直且保持AC平行于OQ。关于线框中的感应电流,以下说法中正确的是BC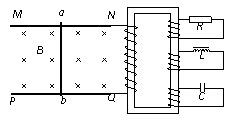 如图所示,MN和PQ为处于同一水平面内的两根平行的光滑金属导轨,导轨的电阻不计.垂直导轨放置一根电阻不变的金属棒ab,金属棒与导轨接触良好.N、Q端接理想变压器的原线圈,理想变压器的输出端有三组副线圈,分别接电阻元件R、电感元件L(电阻不为零)和电容元件C.在水平金属导轨之间加竖直向下的磁感应强度随时间均匀增加的匀强磁场,若用IR、IL、Ic分别表示通过R、L和C的电流,则下列判断正确的是AC
如图所示,MN和PQ为处于同一水平面内的两根平行的光滑金属导轨,导轨的电阻不计.垂直导轨放置一根电阻不变的金属棒ab,金属棒与导轨接触良好.N、Q端接理想变压器的原线圈,理想变压器的输出端有三组副线圈,分别接电阻元件R、电感元件L(电阻不为零)和电容元件C.在水平金属导轨之间加竖直向下的磁感应强度随时间均匀增加的匀强磁场,若用IR、IL、Ic分别表示通过R、L和C的电流,则下列判断正确的是AC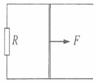 A.恒力F与安培力做的功之和等于电路中产生的电能与金属棒获得的动能和
A.恒力F与安培力做的功之和等于电路中产生的电能与金属棒获得的动能和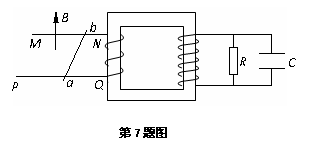 如图所示,MN和PQ为两根足够长的水平光滑金属导轨,导轨电阻不计,变压器为理想变压器,现在水平导轨部分加一竖直向上的匀强磁场,金属棒ab与导轨电接触良好,则以下说法正确的是
(
)CD
如图所示,MN和PQ为两根足够长的水平光滑金属导轨,导轨电阻不计,变压器为理想变压器,现在水平导轨部分加一竖直向上的匀强磁场,金属棒ab与导轨电接触良好,则以下说法正确的是
(
)CD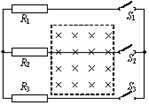 两金属棒和三根电阻丝如图连接,虚线框内存在均匀变化的匀强磁场,三根电阻丝的电阻大小之比R1:R2:R3=1:2:3,金属棒电阻不计。当S1、S2闭合,S3 断开时,闭合的回路中感应电流为I,当S2、S3闭合,S1 断开时,闭合的回路中感应电流为5I,当S1、S3闭合,S2 断开时,闭合的回路中感应电流是[ ]D
两金属棒和三根电阻丝如图连接,虚线框内存在均匀变化的匀强磁场,三根电阻丝的电阻大小之比R1:R2:R3=1:2:3,金属棒电阻不计。当S1、S2闭合,S3 断开时,闭合的回路中感应电流为I,当S2、S3闭合,S1 断开时,闭合的回路中感应电流为5I,当S1、S3闭合,S2 断开时,闭合的回路中感应电流是[ ]D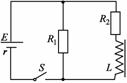 如图所示的电路中,电源电动势为E,内阻r不能忽略.R1和R2是两个定值电阻,L是一个自感系数较大的线圈.开关S原来是断开的.从开关S闭合到电路中电流达到稳定的时间内,通过R1的电流I1和通过R2的电流I2的变化情况是AC
如图所示的电路中,电源电动势为E,内阻r不能忽略.R1和R2是两个定值电阻,L是一个自感系数较大的线圈.开关S原来是断开的.从开关S闭合到电路中电流达到稳定的时间内,通过R1的电流I1和通过R2的电流I2的变化情况是AC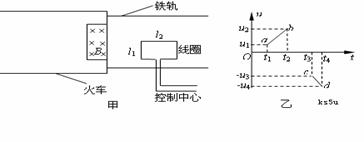 A.在t1~t2时间内做匀加速直线运动
A.在t1~t2时间内做匀加速直线运动