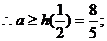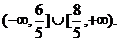高考数学第一轮复习---函数最值的应用
一、最值综合与应用问题:
1.最值综合问题:这是中学数学最重要的题型之一,题型非常广泛.
①几何图形的最值问题:在平几、立几、解几图形中求解面积、体积、距离及各种几何量的最大、最小值;
②代数中的最值问题:求解方程(或不等式)的最大、最小解,数列的最大、最小项,变量或代数式的最大、最小取值,等等;
2.最值应用问题:这是应用问题中最典型的内容,如求解利润、费用的最大与最小,用料,时间最少,流量、销量最大,选取的方法最多、最少等,都是常见的应用问题。
(二)学习要点:
在中学数学范围内,最值综合与应用问题几乎都要运用函数的思想与方法解决,解答程序是:
①正确选择变量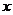 作自变量,根据问题的条件将问题转化为函数,建立函数的解析式
作自变量,根据问题的条件将问题转化为函数,建立函数的解析式 ,并求函数的(实际型)定义域;
,并求函数的(实际型)定义域;
②求函数 的极值,并结合函数的定义域得到函数的最值;
的极值,并结合函数的定义域得到函数的最值;
|

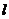 表示成这个角
表示成这个角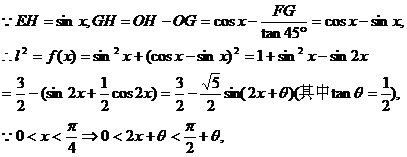
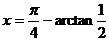 时,
时,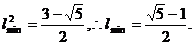
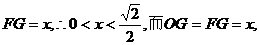
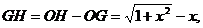
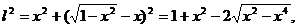
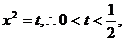
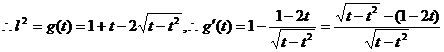
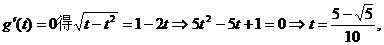
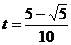 的左、右两侧取定义域内两点,如取
的左、右两侧取定义域内两点,如取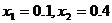
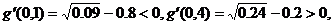
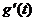 的值在
的值在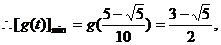
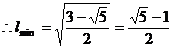 .
.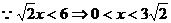
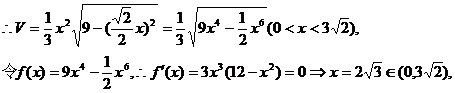
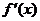 左正右负,∴当
左正右负,∴当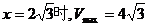 .
.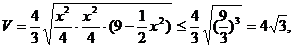
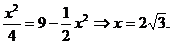
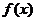 是定义在
是定义在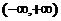 上以2为周期的周期函数,且
上以2为周期的周期函数,且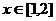 时
时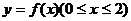 的图象上,求这个矩形面积的最大值.
的图象上,求这个矩形面积的最大值.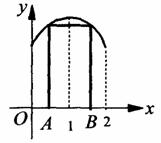
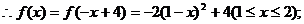
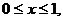 则
则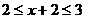 ,
, 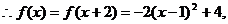
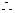 当
当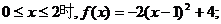

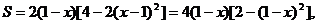
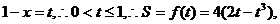
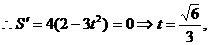 且
且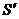 左正右负,
左正右负,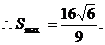
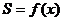 的值域时,换元这一步是很重要的想法,这样大大降低了运算量.
的值域时,换元这一步是很重要的想法,这样大大降低了运算量.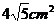 的面积,问应如何设计十字型宽
的面积,问应如何设计十字型宽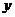 ,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.
,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.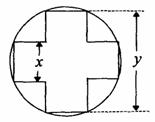
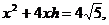 即
即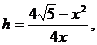
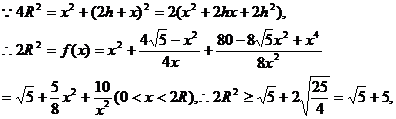
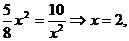
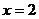 时R2最小,即R最小,从而周长
时R2最小,即R最小,从而周长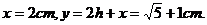
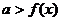 对
对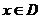 恒成立
恒成立
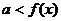 对
对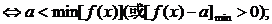
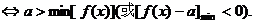

 取何值,直线
取何值,直线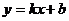 与双曲线
与双曲线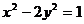 总有公共点,求实数
总有公共点,求实数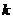 的取值范围.
的取值范围. 对
对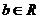 恒成立”.
恒成立”.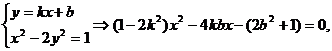
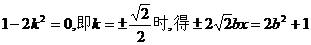 ,显然当
,显然当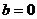 时方程无解,命题不成立;
时方程无解,命题不成立;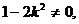 方程为一元二次方程,
方程为一元二次方程,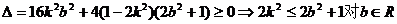 恒成立,
恒成立,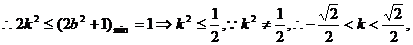
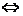 不等式
不等式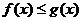 有角,这是“存在”性问题.
有角,这是“存在”性问题.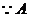 ≠
≠ 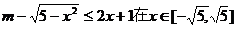 内有解,
内有解,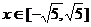 ,使得
,使得



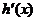 的值在
的值在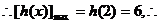 实数
实数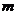 的取值范围是
的取值范围是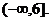
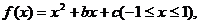 若
若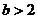 ,问是否存在
,问是否存在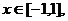 使得
使得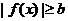 ?说明理由.
?说明理由.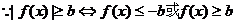 ,
,
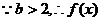 的对称轴
的对称轴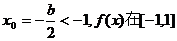 内单调递增,
内单调递增,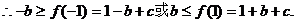 得
得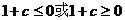 ,
,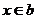 ,使得
,使得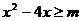 对任意
对任意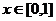 恒成立,则实数
恒成立,则实数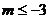 B.
B.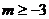
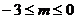 D.
D.
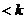 成立,则实数
成立,则实数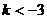 B.
B.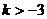 C.
C.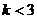 D.
D.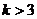
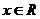 ,如果
,如果 恒成立,那么 ( )
恒成立,那么 ( )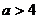 B.
B.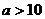 C.
C.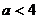 D.
D.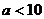
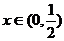 时总有
时总有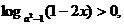 则实数
则实数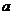 的取值范围是 ( )
的取值范围是 ( )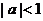 B.
B. C.
C. D.
D.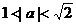
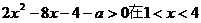 内有解,则实数
内有解,则实数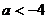 B.
B.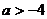 C.
C.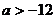 D.
D.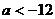
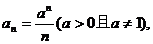 若
若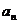 的每一项总小于它的后面的项,则
的每一项总小于它的后面的项,则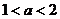 B.
B.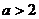 C.
C.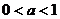 D.
D.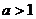
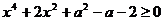 对任意实数
对任意实数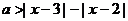 的解集为空集,则实数
的解集为空集,则实数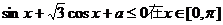 内有解,则实数
内有解,则实数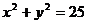 的割线与该圆交于A、B两点,求△AOB的面积的最大值(O为原点)及此时割线AB的方程.
的割线与该圆交于A、B两点,求△AOB的面积的最大值(O为原点)及此时割线AB的方程.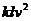 ,其中
,其中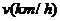 是车速,
是车速,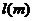 是平均车身长度,
是平均车身长度,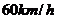 时,安全车距为
时,安全车距为
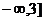 的单调减函数
的单调减函数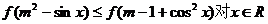 恒成立,求
恒成立,求
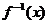 ;
;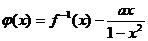 在
在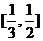 上是单调函数,求实数
上是单调函数,求实数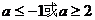 , 8.
, 8.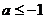 , 9.
, 9.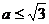 ,10.R2 .
,10.R2 .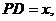 底半径为
底半径为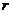 ,
,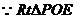 ∽
∽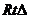 PAD,且OE=OD=1,
PAD,且OE=OD=1,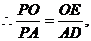 即
即
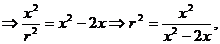

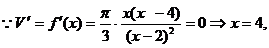
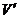 的值在
的值在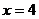 处左负右正,
处左负右正,
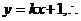 O到AB的距离
O到AB的距离
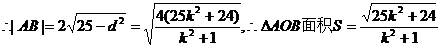

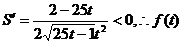 单调递减,
单调递减,
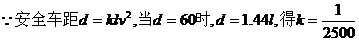 ,
,
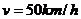 时等号成立. 当
时等号成立. 当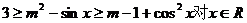 恒成立,
恒成立, ③;
③;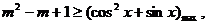

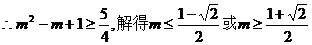 ④;
④;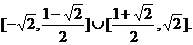
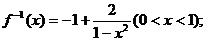
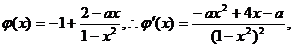
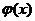 在
在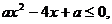 即
即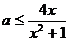 对于
对于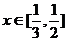 恒成立,记
恒成立,记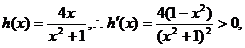
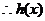 在
在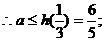
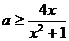 对
对