摘要：1．“恒成立 与“存在 是参数讨论中的两类非常重要的问题.而通过求函数的最值是解决这两类问题的重要方法.在具体解决问题时又有两条基本思路: ①将“参数 与“变量 分离在不等号的两边.然后变量形成的函数的最值,②“参数 与“变量 不分离.将整个式子看成一个函数.并求它的最值.
网址：http://m.1010jiajiao.com/timu_id_23913[举报]
（2011•宁德模拟）由方程2x|x|-y=1所确定的x，y的函数关系记为y=f（x）．给出如下结论：
①f（x）是R上的单调递增函数；
②对于任意x∈R，f（x）+f（-x）=-2恒成立；
③存在x0∈（-1，0），使得过点A（1，f（1）），B（x0，f（x0））的直线与曲线f（x）恰有两个公共点．
其中正确的结论为
查看习题详情和答案>>
①f（x）是R上的单调递增函数；
②对于任意x∈R，f（x）+f（-x）=-2恒成立；
③存在x0∈（-1，0），使得过点A（1，f（1）），B（x0，f（x0））的直线与曲线f（x）恰有两个公共点．
其中正确的结论为
①②③
①②③
（写出所有正确结论的序号）．由方程
所确定的
的函数关系记为
.给出如下结论：
① 
是
上的单调递增函数；
②对于任意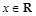
，
恒成立；
③存在
，使得过点
，
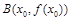的直线与曲线恰有两个公共点．
其中正确的结论为 (写出所有正确结论的序号) ．
查看习题详情和答案>>
如下图所示,在直角坐标系
中,射线
在第一象限,且与
轴的正半轴成定角
,动点
在射线上运动,动点
在
轴的正半轴上运动,
的面积为
.
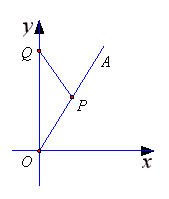
（Ⅰ）求线段
中点
的轨迹
的方程;
（Ⅱ）
是曲线上的动点, 到轴的距离之和为
,
设
为到轴的距离之积.问:是否存在最大的常数
,
使
恒成立?若存在,求出这个的值;若不存在,请说明理由.
所确定的
的函数关系记为
.给出如下结论：
是
上的单调递增函数； 
，
恒成立；
，使得过点
，
的直线与曲线
的焦点为F，准线为l，过点F的直线斜率为k，且与抛物线交于A；B两点，P在准线l上.
)，试问是否存在常数λ；使等式
恒成立?若存在，求出λ的值；若不存在，说明理由.