5.构造函数证明不等式.
典型例题
例7.(2006年天津卷)函数 的定义域为开区间
的定义域为开区间 ,导函数
,导函数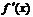 在
在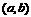 内的图象如图所示,则函数
内的图象如图所示,则函数 在开区间
在开区间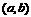 内有极小值点( )
内有极小值点( )
A.1个
 B.2个
B.2个
C.3个
D. 4个
[考查目的]本题主要考查函数的导数和函数图象性质等基础知识的应用能力.
[解答过程]由图象可见,在区间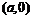 内的图象上有一个极小值点.
内的图象上有一个极小值点.
故选A.
例8 .(2007年全国一)设函数 在
在 及
及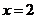 时取得极值.
时取得极值.
(Ⅰ)求a、b的值;
(Ⅱ)若对于任意的 ,都有
,都有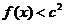 成立,求c的取值范围.
成立,求c的取值范围.
思路启迪:利用函数 在
在 及
及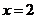 时取得极值构造方程组求a、b的值.
时取得极值构造方程组求a、b的值.
解答过程:(Ⅰ) ,
,
因为函数 在
在 及
及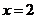 取得极值,则有
取得极值,则有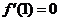 ,
, .
.
即
解得 ,
,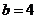 .
.
(Ⅱ)由(Ⅰ)可知, ,
,
 .
.
当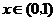 时,
时,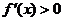 ;
;
当 时,
时, ;
;
当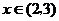 时,
时,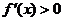 .
.
所以,当 时,
时, 取得极大值
取得极大值 ,又
,又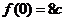 ,
, .
.
则当 时,
时, 的最大值为
的最大值为 .
.
因为对于任意的 ,有
,有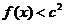 恒成立,
恒成立,
所以  ,
,
解得  或
或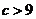 ,
,
因此 的取值范围为
的取值范围为 .
.
例9.函数 的值域是_____________.
的值域是_____________.
思路启迪:求函数的值域,是中学数学中的难点,一般可以通过图象观察或利用不等式性质求解,也可以利用函数的单调性求出最大、最小值。此例的形式结构较为复杂,采用导数法求解较为容易。
解答过程:由 得,
得,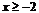 ,即函数的定义域为
,即函数的定义域为 .
.
 ,
,
又 ,
,
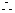 当
当 时,
时,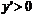 ,
,
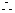 函数
函数 在
在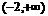 上是增函数,而
上是增函数,而 ,
, 的值域是
的值域是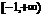 .
.
例10.(2006年天津卷)已知函数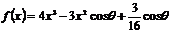 ,其中
,其中 为参数,且
为参数,且 .
.
(1)当时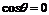 ,判断函数
,判断函数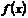 是否有极值;
是否有极值;
(2)要使函数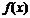 的极小值大于零,求参数
的极小值大于零,求参数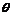 的取值范围;
的取值范围;
(3)若对(2)中所求的取值范围内的任意参数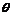 ,函数
,函数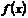 在区间
在区间 内都是增函数,求实数
内都是增函数,求实数 的取值范围.
的取值范围.
[考查目的]本小题主要考查运用导数研究三角函数和函数的单调性及极值、解不等式等基础知识,考查综合分析和解决问题的能力,以及分类讨论的数学思想方法.
[解答过程](Ⅰ)当 时,
时,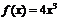 ,则
,则 在
在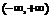 内是增函数,故无极值.
内是增函数,故无极值.
(Ⅱ)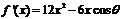 ,令
,令 ,得
,得 .
.
由(Ⅰ),只需分下面两种情况讨论.
①当
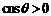 时,随x的变化
时,随x的变化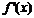 的符号及
的符号及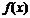 的变化情况如下表:
的变化情况如下表:
|
x |
 |
0 |
 |
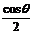 |
 |
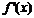 |
+ |
0 |
- |
0 |
+ |
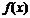 |
↗ |
极大值 |
↘ |
极小值 |
↗ |
因此,函数 在
在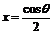 处取得极小值
处取得极小值 ,且
,且 .
.
要使 ,必有
,必有 ,可得
,可得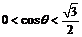 .
.
由于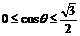 ,故
,故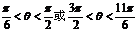 .
.
②当时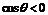 ,随x的变化,
,随x的变化,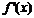 的符号及
的符号及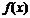 的变化情况如下表:
的变化情况如下表:
 |
 |
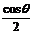 |
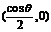 |
 |
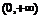 |
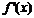 |
+ |
0 |
- |
0 |
+ |
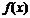 |
 |
极大值 |
 |
极小值 |
 |
因此,函数 处取得极小值
处取得极小值 ,且
,且
若 ,则
,则 .矛盾.所以当
.矛盾.所以当 时,
时,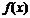 的极小值不会大于零.
的极小值不会大于零.
综上,要使函数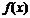 在
在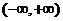 内的极小值大于零,参数
内的极小值大于零,参数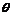 的取值范围为
的取值范围为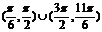 .
.
(III)解:由(II)知,函数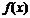 在区间
在区间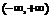 与
与 内都是增函数。
内都是增函数。
由题设,函数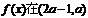 内是增函数,则a须满足不等式组
内是增函数,则a须满足不等式组

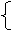
 或
或 
由(II),参数时 时,
时,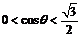 .要使不等式
.要使不等式 关于参数
关于参数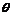 恒成立,必有
恒成立,必有 ,即
,即 .
.
综上,解得 或
或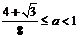 .
.
所以 的取值范围是
的取值范围是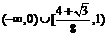 .
.
例11.(2006年山东卷)设函数f(x)=ax-(a+1)ln(x+1),其中a -1,求f(x)的单调区间.
-1,求f(x)的单调区间.
[考查目的]本题考查了函数的导数求法,函数的极值的判定,考查了应用数形结合的数学思想分析问题解决问题的能力
[解答过程]由已知得函数 的定义域为
的定义域为 ,且
,且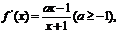
(1)当 时,
时, 函数
函数 在
在 上单调递减,
上单调递减,
(2)当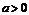 时,由
时,由 解得
解得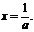
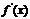 、
、 随
随 的变化情况如下表
的变化情况如下表
 |
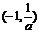 |
 |
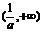 |
 |
- |
0 |
+ |
 |
 |
极小值 |
 |
从上表可知
当 时,
时, 函数
函数 在
在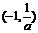 上单调递减.
上单调递减.
当 时,
时,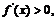 函数
函数 在
在 上单调递增.
上单调递增.
综上所述:当 时,函数
时,函数 在
在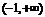 上单调递减.
上单调递减.
当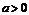 时,函数
时,函数 在
在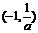 上单调递减,函数
上单调递减,函数 在
在 上单调递增.
上单调递增.
 例12.(2006年北京卷)已知函数
例12.(2006年北京卷)已知函数 在点
在点 处取得极大值
处取得极大值 ,其导函数
,其导函数 的图象经过点
的图象经过点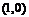 ,
, ,如图所示.求:
,如图所示.求:
(Ⅰ)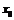 的值;
的值;
(Ⅱ) 的值.
的值.
[考查目的]本小题考查了函数的导数,函数的极值的判定,闭区间上二次函数的最值, 函数与方程的转化等基础知识的综合应用,考查了应用数形结合的数学思想分析问题解决问题的能力
[解答过程]解法一:(Ⅰ)由图像可知,在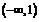 上
上
 ,在
,在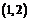 上
上 ,在
,在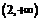 上
上 ,
,
故 在
在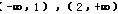 上递增,在
上递增,在 上递减,
上递减,
因此 在
在 处取得极大值,所以
处取得极大值,所以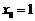
(Ⅱ)
由
得
解得
解法二:(Ⅰ)同解法一
(Ⅱ)设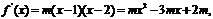
又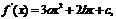
所以

由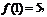 即
即 得
得
所以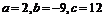
例13.(2006年湖北卷)设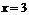 是函数
是函数 的一个极值点.
的一个极值点.
(Ⅰ)求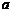 与
与 的关系式(用
的关系式(用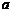 表示
表示 ),并求
),并求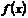 的单调区间;
的单调区间;
(Ⅱ)设 ,
,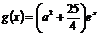 .若存在
.若存在 使得
使得 成立,求
成立,求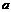 的取值范围.
的取值范围.
[考查目的]本小题主要考查函数、不等式和导数的应用等知识,考查综合运用数学知识解决问题的能力.
[解答过程](Ⅰ)f `(x)=-[x2+(a-2)x+b-a ]e3-x,
由f `(3)=0,得 -[32+(a-2)3+b-a ]e3-3=0,即得b=-3-2a,
则 f `(x)=[x2+(a-2)x-3-2a-a ]e3-x
=-[x2+(a-2)x-3-3a ]e3-x=-(x-3)(x+a+1)e3-x.
令f `(x)=0,得x1=3或x2=-a-1,由于x=3是极值点,
所以x+a+1≠0,那么a≠-4.
当a<-4时,x2>3=x1,则
在区间(-∞,3)上,f `(x)<0, f (x)为减函数;
在区间(3,―a―1)上,f `(x)>0,f (x)为增函数;
在区间(―a―1,+∞)上,f `(x)<0,f (x)为减函数.
当a>-4时,x2<3=x1,则
在区间(-∞,―a―1)上,f `(x)<0, f (x)为减函数;
在区间(―a―1,3)上,f `(x)>0,f (x)为增函数;
在区间(3,+∞)上,f `(x)<0,f (x)为减函数.
(Ⅱ)由(Ⅰ)知,当a>0时,f (x)在区间(0,3)上的单调递增,在区间(3,4)上单调递减,那么f (x)在区间[0,4]上的值域是[min(f (0),f (4) ),f (3)],
而f (0)=-(2a+3)e3<0,f (4)=(2a+13)e-1>0,f (3)=a+6,
那么f (x)在区间[0,4]上的值域是[-(2a+3)e3,a+6].
又 在区间[0,4]上是增函数,
在区间[0,4]上是增函数,
且它在区间[0,4]上的值域是[a2+ ,(a2+
,(a2+ )e4],
)e4],
由于(a2+ )-(a+6)=a2-a+
)-(a+6)=a2-a+ =(
=(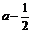 )2≥0,所以只须仅须
)2≥0,所以只须仅须
(a2+ )-(a+6)<1且a>0,解得0<a<
)-(a+6)<1且a>0,解得0<a<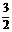 .
.
故a的取值范围是(0,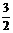 ).
).
例14 (2007年全国二)
已知函数
在 处取得极大值,在
处取得极大值,在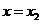 处取得极小值,且
处取得极小值,且 .
.
(1)证明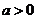 ;
;
(2)若z=a+2b,求z的取值范围。
[解答过程]求函数 的导数
的导数 .
.
(Ⅰ)由函数 在
在 处取得极大值,在
处取得极大值,在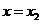 处取得极小值,知
处取得极小值,知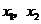 是
是 的两个根.
的两个根.
所以
当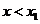 时,
时, 为增函数,
为增函数,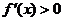 ,由
,由 ,
,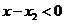 得
得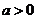 .
.
(Ⅱ)在题设下, 等价于
等价于 即
即 .
.
化简得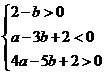 .
.
此不等式组表示的区域为平面 上三条直线:
上三条直线: .
.
所围成的 的内部,其三个顶点分别为:
的内部,其三个顶点分别为: .
.

 在这三点的值依次为
在这三点的值依次为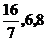 .
.
所以 的取值范围为
的取值范围为 .
.
小结:本题的新颖之处在把函数的导数与线性
规划有机结合.
考点4 导数的实际应用
建立函数模型,利用
典型例题
例15. (2007年重庆文)
用长为18 cm的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
[考查目的]本小题主要考查函数、导数及其应用等基本知识,考查运用数学知识分析和解决实际问题的能力.
[解答过程]设长方体的宽为x(m),则长为2x(m),高为
 .
.
故长方体的体积为

从而
令V′(x)=0,解得x=0(舍去)或x=1,因此x=1.
当0<x<1时,V′(x)>0;当1<x<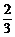 时,V′(x)<0,
时,V′(x)<0,
故在x=1处V(x)取得极大值,并且这个极大值就是V(x)的最大值。
从而最大体积V=V′(x)=9×12-6×13(m3),此时长方体的长为2 m,高为1.5 m.
答:当长方体的长为2 m时,宽为1 m,高为1.5 m时,体积最大,最大体积为3 m3。
例16.(2006年福建卷)统计表明,某种型号的汽车在匀速行驶中每小时的耗
油量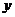 (升)关于行驶速度
(升)关于行驶速度 (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为:
 已知甲、乙两地相距100千米.
已知甲、乙两地相距100千米.
(I)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(II)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
[考查目的]本小题主要考查函数、导数及其应用等基本知识,考查运用数学知识分析和解决实际问题的能力.
[解答过程](I)当 时,汽车从甲地到乙地行驶了
时,汽车从甲地到乙地行驶了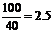 小时,
小时,
要耗没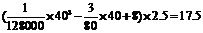 (升).
(升).
答:当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地耗油17.5升。
(II)当速度为 千米/小时时,汽车从甲地到乙地行驶了
千米/小时时,汽车从甲地到乙地行驶了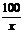 小时,设耗油量为
小时,设耗油量为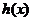 升,依题意得
升,依题意得

令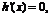 得
得
当 时,
时, 是减函数;当
是减函数;当 时,
时, 是增函数.
是增函数.
当 时,
时, 取到极小值
取到极小值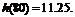
因为 在
在 上只有一个极值,所以它是最小值.
上只有一个极值,所以它是最小值.
 答:当汽车以80千米/小时的速度匀速行驶时,从甲地到乙地耗油最少,最少为11.25升.
答:当汽车以80千米/小时的速度匀速行驶时,从甲地到乙地耗油最少,最少为11.25升.
 ,
,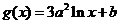 ,其中
,其中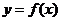 ,
, 有公共点,且在该点处的切线相同.用
有公共点,且在该点处的切线相同.用 ,并求
,并求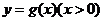 在公共点
在公共点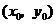 处的切线相同.
处的切线相同. ,
, ,由题意
,由题意 ,
, .
. 由
由 得:
得: ,或
,或 (舍去).
(舍去).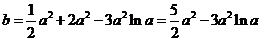 .
. ,则
,则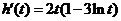 .于是当
.于是当 ,即
,即 时,
时,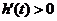 ;当
;当 ,即
,即 时,
时, .故
.故 在
在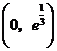 为增函数,
为增函数,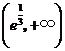 为减函数,∴
为减函数,∴ 的最大值为
的最大值为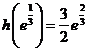 .
.
 在
在 ,
,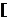 0,1]上递增,[1,2]上递减,[2,3]上递增;∴当
0,1]上递增,[1,2]上递减,[2,3]上递增;∴当 在
在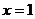 处有极值10,则
处有极值10,则
 ,∴
,∴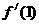 =
= ①
① ②
由①②得:
②
由①②得: 或
或
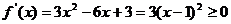 ,此时函数
,此时函数 ,函数
,函数 [xf(x)]/ ≤0
[xf(x)]/ ≤0 ②
②
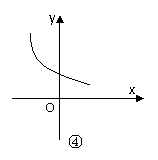
 A.①② B.①③ C.②③
D.③④
A.①② B.①③ C.②③
D.③④

 若
若 在
在 是增函数,求实数
是增函数,求实数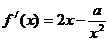 ≥0在
≥0在 在
在 在
在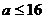 。
。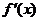 是
是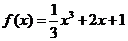 的导函数,则
的导函数,则 的值是 .
的值是 .
 ,集合M=
,集合M= ,P=
,P= ,若M
,若M P,则实数a的取值范围是 ( )
P,则实数a的取值范围是 ( ) 
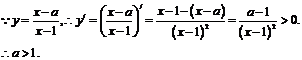

 在区间
在区间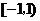 ,
, 内各有一个极值点.
内各有一个极值点. 的最大值;
的最大值;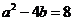 时,设函数
时,设函数 处的切线为
处的切线为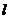 ,若
,若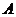 处穿过函数
处穿过函数
 在
在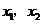 (
( ),则
),则 ,且
,且 .于是
.于是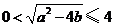 ,
, ,且当
,且当
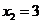 ,即
,即 ,
, 时等号成立.故
时等号成立.故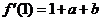 知
知 处的切线
处的切线 ,即
,即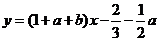 ,
, 处空过
处空过 在
在 的极值点.
的极值点. ,且
,且 .
.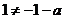 ,则
,则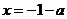 都是
都是 ,即
,即 ,故
,故 .
. .
. (
( ).
).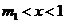 时,
时, ,当
,当 时,
时,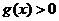 ;
;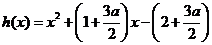 ,则
,则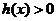 ,当
,当 ,当
,当 知
知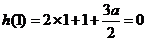 ,
,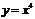 的一条切线
的一条切线 与直线
与直线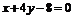 垂直,则
垂直,则 B.
B.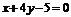
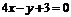 D.
D.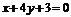
 垂直的直线
垂直的直线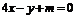 ,即
,即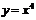 在某一点的导数为4,而
在某一点的导数为4,而 ,所以
,所以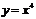 在(1,1)处导数为4,此点的切线为
在(1,1)处导数为4,此点的切线为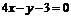 .
. =0相切的直线的方程为 ( )
=0相切的直线的方程为 ( )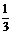 x B. y=-3x或y=-
x B. y=-3x或y=-
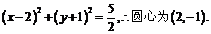
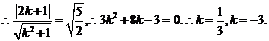

 由
由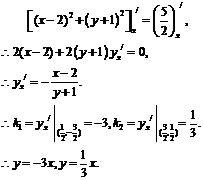
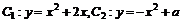 ,
,  ,
, 有且只有一条公切线,求出此时公切线的方程.
有且只有一条公切线,求出此时公切线的方程. 的导数为
的导数为 ,曲线
,曲线 在点P(
在点P( )处的切线方程为
)处的切线方程为 ,即
,即
 ①
①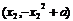 的切线方程是
的切线方程是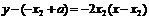 即
即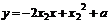 ②
② ,消去
,消去 得方程,
得方程,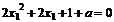
 ,即
,即 时,解得
时,解得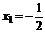 ,此时点P、Q重合.
,此时点P、Q重合. .
.