摘要：f(x)是定义在上的非负可导函数.且满足xf/≤0,对任意正数a.b,若a＜b.则必有 A.af(b) ≤bf(a) B.bf(a) ≤af(b) C.af(a) ≤f(b) D.bf(b) ≤f(a) 解析:xf/≤0[xf(x)]/ ≤0函数F上为常函数或递减. 又0<a＜b且f(x)非负.于是有:af≥0 ① ② ①②两式相乘得: af.故选A.
网址：http://m.1010jiajiao.com/timu_id_4051235[举报]
f(x)是定义在(0，±∞)上的非负可导函数，且满足xf(x)＋f(x)≤0，对任意正数a、b，若a＜b，则必有
[ ]
A．
af(b)≤bf(a)
B．
bf(a)≤af(b)
C．
af(a)≤f(b)
D．
bf(b)≤f(a)
f(x)是定义在(0，＋∞)上的非负可导函数，且满足xf′(x)＋f(x)≤0，对任意正数a，b，若a<b，则必有( )
A．af(b)≤bf(a) B．bf(a)≤af(b)
C．af(a)≤f(b) D．bf(b)≤f(a)
查看习题详情和答案>>f(x)是定义在(0，＋∞)上的非负可导函数，且满足
，对任意正数a，b，若a<b，则必有( )
A．af(b)＜bf(a) B．bf(a) ＜af(b) C．af(a)＜bf (b) D．bf(b) ＜a f(a)
查看习题详情和答案>>
，对任意正数a，b，若a<b，则必有( )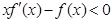
，对任意正数a，b，若a<b，则必有( )