3.(08广东广州)25、(2008广州)(14分)如图11,在梯形ABCD中,AD∥BC,AB=AD=DC=2cm,BC=4cm,在等腰△PQR中,∠QPR=120°,底边QR=6cm,点B、C、Q、R在同一直线l上,且C、Q两点重合,如果等腰△PQR以1cm/秒的速度沿直线l箭头所示方向匀速运动,t秒时梯形ABCD与等腰△PQR重合部分的面积记为S平方厘米
(1)当t=4时,求S的值
(2)当 ,求S与t的函数关系式,并求出S的最大值
,求S与t的函数关系式,并求出S的最大值
|
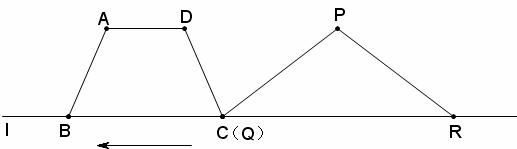
(08广东广州25题解析)25.(1)t=4时,Q与B重合,P与D重合,
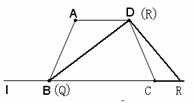 重合部分是
重合部分是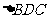 =
=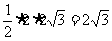
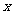 元.求:
元.求: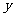 (间)关于
(间)关于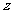 (元)关于
(元)关于 (元)关于
(元)关于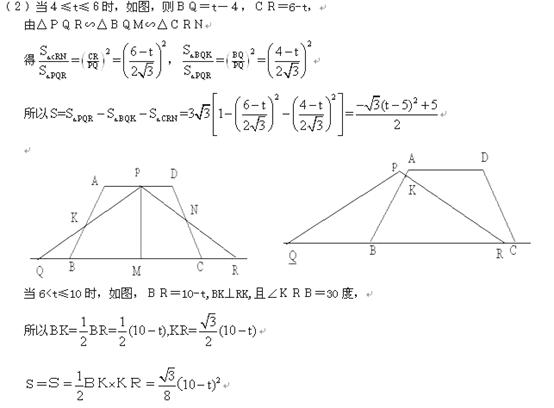 (08广东深圳)22.如图9,在平面直角坐标系中,二次函数
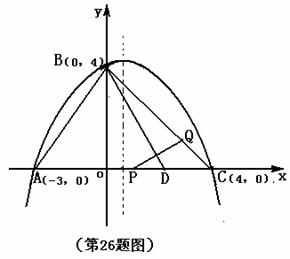
(08广东深圳)22.如图9,在平面直角坐标系中,二次函数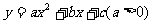 的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),OB=OC ,tan∠ACO=
的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),OB=OC ,tan∠ACO=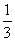 .
(1)求这个二次函数的表达式.
.
(1)求这个二次函数的表达式.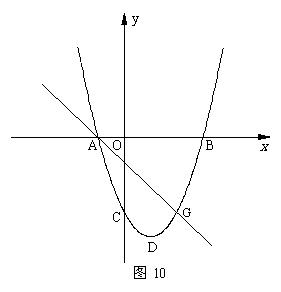
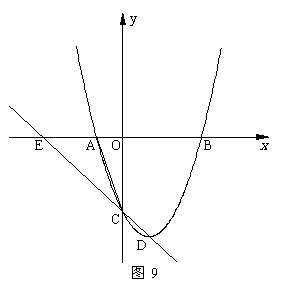 (4)如图10,若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,当点P运动到什么位置时,△APG的面积最大?求出此时P点的坐标和△APG的最大面积.
(4)如图10,若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,当点P运动到什么位置时,△APG的面积最大?求出此时P点的坐标和△APG的最大面积.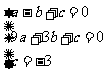 ……………………2分
……………………2分 ……………………3分
……………………3分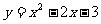 ……………………3分
……………………3分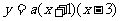 ……………………2分
……………………2分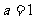 ……………………3分
……………………3分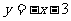
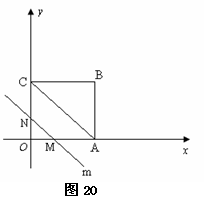
 (3)如图,①当直线MN在x轴上方时,设圆的半径为R(R>0),则N(R+1,R),
(3)如图,①当直线MN在x轴上方时,设圆的半径为R(R>0),则N(R+1,R),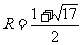 …………6分
…………6分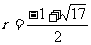 ………7分
………7分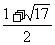 或
或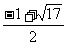 . ……………7分
. ……………7分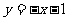 .……………8分
.……………8分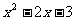 ),则Q(x,-x-1),PQ
),则Q(x,-x-1),PQ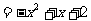 .
.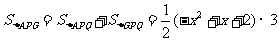 ……………………9分
……………………9分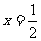 时,△APG的面积最大
时,△APG的面积最大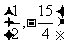 ,
, .
……………………10分
.
……………………10分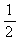 AC;
AC;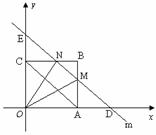 (3) 当0<t≤4时,OM=t.
(3) 当0<t≤4时,OM=t.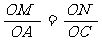 ,
,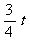 ,S=
,S=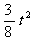 . ···································· 6分
. ···································· 6分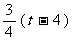 ,∴ BM=6-
,∴ BM=6-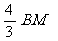 =8-t,∴ CN=t-4. ·································· 8分
=8-t,∴ CN=t-4. ·································· 8分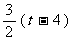 -
-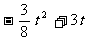 . ··························································································· 10分
. ··························································································· 10分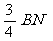 =6-
=6-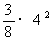 =6; ················ 11分
=6; ················ 11分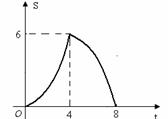 综上,当t=4时,S有最大值6. ······································································· 12分
综上,当t=4时,S有最大值6. ······································································· 12分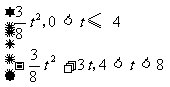
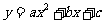 的对称轴为
的对称轴为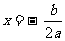 )
)
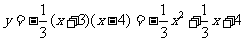
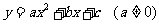 ,
, 解得
解得
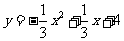
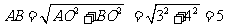
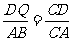 即
即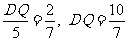
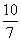 =
=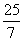 ,
,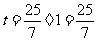
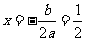
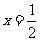 对称
对称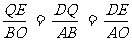 即
即 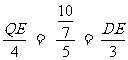
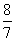 ,DE=
,DE=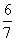 ,所以OE = OD + DE=2+
,所以OE = OD + DE=2+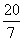 ,所以Q(
,所以Q(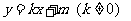
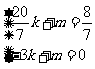 由此得
由此得 
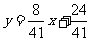 联立
联立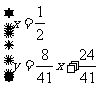
 由此得
由此得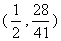
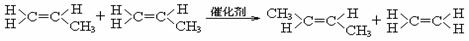
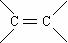 提示:有机物分子结构中的
比-OH更容易被氧化。
提示:有机物分子结构中的
比-OH更容易被氧化。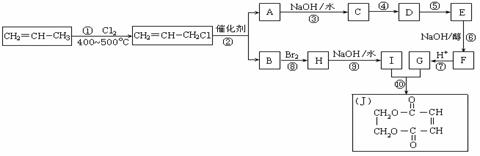
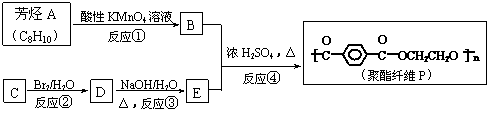 (1)A的结构简式是
,C的结构简式是
。
(1)A的结构简式是
,C的结构简式是
。 反应④的化学方程式是 。
反应④的化学方程式是 。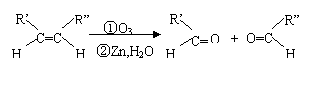
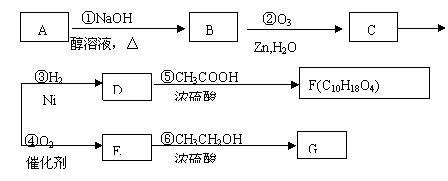
 (3)D
F的反应方程式是___________________________
(3)D
F的反应方程式是___________________________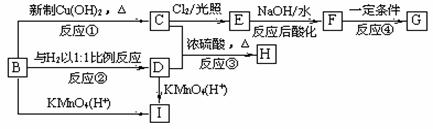
 、
;
、
;