题目内容
10.将一质量为m的木箱放在水平桌面上,现对木箱施加一斜向右下方的恒力,使木箱由静止开始以恒定的加速度a沿水平桌面向右做匀加速直线运动.已知恒力与水平方向的夹角为θ,木箱与桌面间的动摩擦因数为μ,重力加速度为g.则木箱向右运动位移x的过程中,下列说法正确的是( )| A. | 恒力所做的功为$\frac{ma-μgx}{1+μtanθ}$ | |
| B. | 恒力所做的功为$\frac{ma+μmg}{cosθ-μsinθ}$ | |
| C. | 木箱克服摩擦力做的功为μ(mg+macos)x | |
| D. | 木箱克服摩擦力做的功为$\frac{μma-gcotθ}{cotθ-μ}x$ |
分析 对物体受力分析,根据牛顿第二定律求得拉力和物体受到的摩擦力,根据W=Fxcosθ求得拉力和摩擦力做功
解答 解:以木箱为研究对象,竖直方向有:Fsin θ+mg=FN
水平方向有:Fcos θ-μFN=ma
联立解得恒力为:F=$\frac{ma+μmg}{cosθ-μsinθ}$
摩擦力为:f=μFN=$\frac{μmasinθ+μmgcosθ}{cosθ-μsinθ}$
则在此过程中恒力做的功为:W=Fxcos θ=$\frac{ma+μmg}{1-μtanθ}x$
木箱克服摩擦力做的功为:Wf=fx=$\frac{μma-gcotθ}{cot-μ}x$,故AC错误,BD正确
故选:BD
点评 本题主要考查了恒力做功,抓住W=Fxcosθ,关键是通过受力分析求得拉力和摩擦力

练习册系列答案
相关题目
1.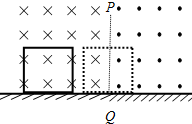 如图所示,在光滑的水平面上方,有两个磁感应强度大小均为B,方向相反的水平匀强磁场.PQ为两个磁场的边界,磁场范围足够大.一个边长为a、质量为m、电阻为R的金属正方形线框,以速度v沿垂直磁场方向从如图实线位置开始向右运动,当线框运动到分别有一半面积在两个磁场中时,线框的速度为$\frac{v}{2}$,则下列说法正确的是( )
如图所示,在光滑的水平面上方,有两个磁感应强度大小均为B,方向相反的水平匀强磁场.PQ为两个磁场的边界,磁场范围足够大.一个边长为a、质量为m、电阻为R的金属正方形线框,以速度v沿垂直磁场方向从如图实线位置开始向右运动,当线框运动到分别有一半面积在两个磁场中时,线框的速度为$\frac{v}{2}$,则下列说法正确的是( )
 如图所示,在光滑的水平面上方,有两个磁感应强度大小均为B,方向相反的水平匀强磁场.PQ为两个磁场的边界,磁场范围足够大.一个边长为a、质量为m、电阻为R的金属正方形线框,以速度v沿垂直磁场方向从如图实线位置开始向右运动,当线框运动到分别有一半面积在两个磁场中时,线框的速度为$\frac{v}{2}$,则下列说法正确的是( )
如图所示,在光滑的水平面上方,有两个磁感应强度大小均为B,方向相反的水平匀强磁场.PQ为两个磁场的边界,磁场范围足够大.一个边长为a、质量为m、电阻为R的金属正方形线框,以速度v沿垂直磁场方向从如图实线位置开始向右运动,当线框运动到分别有一半面积在两个磁场中时,线框的速度为$\frac{v}{2}$,则下列说法正确的是( )| A. | 此时线框的加速度为$\frac{{B}^{2}{a}^{2}v}{2mR}$ | |
| B. | 此过程中通过线框截面的电量为$\frac{B{a}^{2}}{R}$ | |
| C. | 此过程中回路产生的电能为$\frac{3}{8}$mv2 | |
| D. | 此时线框中的电功率为$\frac{{{B}^{2}a}^{2}{v}^{2}}{2R}$ |
18. 如图所示,A、B为两个电荷量相等的正点电荷,a、O、b在点电荷A、B的连线上,c、O、d在连线的中垂线上,Oa=Ob=Oc=Od,则( )
如图所示,A、B为两个电荷量相等的正点电荷,a、O、b在点电荷A、B的连线上,c、O、d在连线的中垂线上,Oa=Ob=Oc=Od,则( )
 如图所示,A、B为两个电荷量相等的正点电荷,a、O、b在点电荷A、B的连线上,c、O、d在连线的中垂线上,Oa=Ob=Oc=Od,则( )
如图所示,A、B为两个电荷量相等的正点电荷,a、O、b在点电荷A、B的连线上,c、O、d在连线的中垂线上,Oa=Ob=Oc=Od,则( )| A. | a、b两点的场强大小、方向都相同 | |
| B. | c、d两点的场强大小相同,方向相反 | |
| C. | 将一个正的试探电荷从a点移动到c点,电场力做正功 | |
| D. | 将一个正的试探电荷从c点移动到O点,电场力不做功 |
5. 如图所示,两光滑且平行的固定水平杆位于同一竖直平面内,两静止小球m1、m2分别穿在两杆上,两球间连接一个保持原长的竖直轻弹簧,现给小球m2一个水平向右的初速度v0.如果两杆足够长,则在此后的运动过程中( )
如图所示,两光滑且平行的固定水平杆位于同一竖直平面内,两静止小球m1、m2分别穿在两杆上,两球间连接一个保持原长的竖直轻弹簧,现给小球m2一个水平向右的初速度v0.如果两杆足够长,则在此后的运动过程中( )
 如图所示,两光滑且平行的固定水平杆位于同一竖直平面内,两静止小球m1、m2分别穿在两杆上,两球间连接一个保持原长的竖直轻弹簧,现给小球m2一个水平向右的初速度v0.如果两杆足够长,则在此后的运动过程中( )
如图所示,两光滑且平行的固定水平杆位于同一竖直平面内,两静止小球m1、m2分别穿在两杆上,两球间连接一个保持原长的竖直轻弹簧,现给小球m2一个水平向右的初速度v0.如果两杆足够长,则在此后的运动过程中( )| A. | m1、m2组成的系统机械能守恒 | |
| B. | 当 m1的速度达到最大时,m2同速度最小 | |
| C. | m1、m2组成的系统动量守恒 | |
| D. | 弹簧最长时,其弹性势能为$\frac{1}{2}$m2v02 |
19.下面各个实例中,机械能守恒的是( )
| A. | 用一细绳吊着一个物体在竖直方向上上下运动过程中,以物体和地球组成系统 | |
| B. | 物体从高处以0.9g的加速度竖直下落 | |
| C. | 铅球运动员抛出的铅球从抛出到落地前的运动 | |
| D. | 拉着一个物体沿光滑的斜面匀速上升 |
 如图所示,甲、乙两个小孩各乘一辆冰车在水平冰面上做游戏,甲和他的冰车总质量共为30kg,乙和他的冰车总质量也为30kg,游戏时,甲推着一个质量为15kg的箱子和他一起以2m/s的速度滑行,乙以同样大小的速度迎面滑来,为了避免相撞,甲突然将箱子沿冰面推给乙,箱子滑到乙处时乙迅速把它抓住,不计冰面的摩擦,
如图所示,甲、乙两个小孩各乘一辆冰车在水平冰面上做游戏,甲和他的冰车总质量共为30kg,乙和他的冰车总质量也为30kg,游戏时,甲推着一个质量为15kg的箱子和他一起以2m/s的速度滑行,乙以同样大小的速度迎面滑来,为了避免相撞,甲突然将箱子沿冰面推给乙,箱子滑到乙处时乙迅速把它抓住,不计冰面的摩擦, 某人身系弹性绳自高空P点自由下落,绳自由长度l0=5.0m,若人自下落直至到达最低点时间为1.0s,则在此过程中,弹性绳给人的冲量大小为多少?已知人的质量为60kg,不计空气阻力,g取10m/s2,可将人视为质点.
某人身系弹性绳自高空P点自由下落,绳自由长度l0=5.0m,若人自下落直至到达最低点时间为1.0s,则在此过程中,弹性绳给人的冲量大小为多少?已知人的质量为60kg,不计空气阻力,g取10m/s2,可将人视为质点.
 如图所示,光滑的轻杆可以绕其一端O,在竖直面内做匀速圆周运动,杆上穿着两个质量均为m=1kg的小球(小球均视为质点,杆与小球之间无摩擦力).小球A与转轴O之间的距离为L=0.3m,小球A与小球B之间距离也为L,长为L的轻绳一端连接小球A另一端连接在O点,小球A和小球B也用长为L的轻绳连接(图中未画出轻绳),两根轻绳能承受的最大张力相同,均为Tmax=110N.(g=10m/s2)
如图所示,光滑的轻杆可以绕其一端O,在竖直面内做匀速圆周运动,杆上穿着两个质量均为m=1kg的小球(小球均视为质点,杆与小球之间无摩擦力).小球A与转轴O之间的距离为L=0.3m,小球A与小球B之间距离也为L,长为L的轻绳一端连接小球A另一端连接在O点,小球A和小球B也用长为L的轻绳连接(图中未画出轻绳),两根轻绳能承受的最大张力相同,均为Tmax=110N.(g=10m/s2)