题目内容
2.如图甲所示,质量m=2.0kg的物体在水平外力的作用下在水平面上运动,已知物体沿x方向和y方向的x-t图象和vy-t图象如图乙、丙所示,t=0时刻,物体位于原点O,g取10m/s2.根据以上条件,求:
(1)t=10s时刻物体的位置坐标;
(2)t=10s时刻物体的速度大小.
分析 (1)根据坐标与时间之间的关系式,代入时间即可得知该时刻对应位置的坐标.
(2)物体在两个方向上均为直线运动,所以坐标的竖直等于在该方向上的位移大小,再结合直线运动的公式,即可得知这两个方向上的速度,再对速度进行合成,可得该时刻的实际速度大小.
解答 解:(1)由于物体运动过程中的坐标与时间的关系为:
在x轴方向上:x=3.0tm
在y轴方向上:vy=0.4t
则有,y=0.2t2m
代入时间t=10 s,可得:
x=3.0t m=3.0×10 m=30 m
y=0.2t2 m=0.2×102 m=20 m
即t=10 s时刻物体的位置坐标为(30 m,20 m).
(2)在x轴方向上:x=3.0tm
在y轴方向上:y=0.2t2m
物体在这两个方向上的运动学公式为:
在x轴方向上:x=v0t
在y轴方向上:vy=at,
则有,y=$\frac{1}{2}$at2;
联立并代入数据得:v0=3.0 m/s,a=0.4 m/s2
当t=10 s时,vy=at=0.4×10 m/s=4.0 m/s
v=$\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5.0m/s
答:(1)t=10s时刻物体的位置坐标为(30 m,20 m).
(2)t=10s时刻物体的速度的大小为5.0m/s.
点评 该题考查了对运动合成与分解的应用和物体位置的求解.要求学生要会在直角坐标系中确定物体位置,会结合位移的定理,了解位置与位移之间的联系,能熟练的应用运动学公式处理有关问题,同时注意直角三角形的知识在正交分解上的应用.

练习册系列答案
相关题目
10.将一质量为m的木箱放在水平桌面上,现对木箱施加一斜向右下方的恒力,使木箱由静止开始以恒定的加速度a沿水平桌面向右做匀加速直线运动.已知恒力与水平方向的夹角为θ,木箱与桌面间的动摩擦因数为μ,重力加速度为g.则木箱向右运动位移x的过程中,下列说法正确的是( )
| A. | 恒力所做的功为$\frac{ma-μgx}{1+μtanθ}$ | |
| B. | 恒力所做的功为$\frac{ma+μmg}{cosθ-μsinθ}$ | |
| C. | 木箱克服摩擦力做的功为μ(mg+macos)x | |
| D. | 木箱克服摩擦力做的功为$\frac{μma-gcotθ}{cotθ-μ}x$ |
17. 如图所示,质量为 M 的楔形物体静止在光滑的水平地面上,其 斜面光滑且足够长,与水平方向的夹角为θ.一个质量为 m 的小 物块从斜面底端沿斜面向上以初速度 v0开始运动.当小物块沿斜面向上运动到最高点时,速度大小为 v,距地面高度为 h,则下列关系式中正确的是( )
如图所示,质量为 M 的楔形物体静止在光滑的水平地面上,其 斜面光滑且足够长,与水平方向的夹角为θ.一个质量为 m 的小 物块从斜面底端沿斜面向上以初速度 v0开始运动.当小物块沿斜面向上运动到最高点时,速度大小为 v,距地面高度为 h,则下列关系式中正确的是( )
 如图所示,质量为 M 的楔形物体静止在光滑的水平地面上,其 斜面光滑且足够长,与水平方向的夹角为θ.一个质量为 m 的小 物块从斜面底端沿斜面向上以初速度 v0开始运动.当小物块沿斜面向上运动到最高点时,速度大小为 v,距地面高度为 h,则下列关系式中正确的是( )
如图所示,质量为 M 的楔形物体静止在光滑的水平地面上,其 斜面光滑且足够长,与水平方向的夹角为θ.一个质量为 m 的小 物块从斜面底端沿斜面向上以初速度 v0开始运动.当小物块沿斜面向上运动到最高点时,速度大小为 v,距地面高度为 h,则下列关系式中正确的是( )| A. | mv0=(m+M )v | B. | mv0cosθ=(m+M )v | ||
| C. | mgh+$\frac{1}{2}$(m+M)v2=$\frac{1}{2}$mv02cos2θ | D. | mgh=$\frac{1}{2}$mv02-$\frac{1}{2}$mv2 |
7. 在光滑水平面上甲、乙两车相向而行,甲的速率为v0,乙的速率也为v0,甲车和车上人的总质量为10m,乙车和车上人及货包的总质量为12m,单个货包质量为$\frac{m}{10}$,为不使两车相撞,乙车上的人以相对地面为v=11v0的速率将货包抛出给甲车上的人,求:为使两车不相撞,乙车上的人应抛出货包的最小数量( )
在光滑水平面上甲、乙两车相向而行,甲的速率为v0,乙的速率也为v0,甲车和车上人的总质量为10m,乙车和车上人及货包的总质量为12m,单个货包质量为$\frac{m}{10}$,为不使两车相撞,乙车上的人以相对地面为v=11v0的速率将货包抛出给甲车上的人,求:为使两车不相撞,乙车上的人应抛出货包的最小数量( )
 在光滑水平面上甲、乙两车相向而行,甲的速率为v0,乙的速率也为v0,甲车和车上人的总质量为10m,乙车和车上人及货包的总质量为12m,单个货包质量为$\frac{m}{10}$,为不使两车相撞,乙车上的人以相对地面为v=11v0的速率将货包抛出给甲车上的人,求:为使两车不相撞,乙车上的人应抛出货包的最小数量( )
在光滑水平面上甲、乙两车相向而行,甲的速率为v0,乙的速率也为v0,甲车和车上人的总质量为10m,乙车和车上人及货包的总质量为12m,单个货包质量为$\frac{m}{10}$,为不使两车相撞,乙车上的人以相对地面为v=11v0的速率将货包抛出给甲车上的人,求:为使两车不相撞,乙车上的人应抛出货包的最小数量( )| A. | 10个 | B. | 11个 | C. | 12个 | D. | 20个 |
14. 用如图所示的实验装置观察光的薄膜干涉现象.点燃酒精灯并在灯芯上洒些盐,竖立着一层肥皂液薄膜的金属丝圈.下面说法正确的是( )
用如图所示的实验装置观察光的薄膜干涉现象.点燃酒精灯并在灯芯上洒些盐,竖立着一层肥皂液薄膜的金属丝圈.下面说法正确的是( )
 用如图所示的实验装置观察光的薄膜干涉现象.点燃酒精灯并在灯芯上洒些盐,竖立着一层肥皂液薄膜的金属丝圈.下面说法正确的是( )
用如图所示的实验装置观察光的薄膜干涉现象.点燃酒精灯并在灯芯上洒些盐,竖立着一层肥皂液薄膜的金属丝圈.下面说法正确的是( )| A. | 当金属丝圈旋转30°时干涉条纹同方向旋转30° | |
| B. | 当金属丝圈旋转45°时干涉条纹同方向旋转90° | |
| C. | 当金属丝圈旋转60°时干涉条纹同方向旋转30° | |
| D. | 干涉条纹保持原来状态不变 |
11.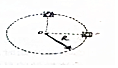 如图所示,质量为m的小球置于正方体的光滑盒子中,盒子的边长略大于球的直径.某同学拿着该盒子在竖直平面内做半径为R的匀速圆周运动,已知重力加速度为g,空气阻力不计,则( )
如图所示,质量为m的小球置于正方体的光滑盒子中,盒子的边长略大于球的直径.某同学拿着该盒子在竖直平面内做半径为R的匀速圆周运动,已知重力加速度为g,空气阻力不计,则( )
 如图所示,质量为m的小球置于正方体的光滑盒子中,盒子的边长略大于球的直径.某同学拿着该盒子在竖直平面内做半径为R的匀速圆周运动,已知重力加速度为g,空气阻力不计,则( )
如图所示,质量为m的小球置于正方体的光滑盒子中,盒子的边长略大于球的直径.某同学拿着该盒子在竖直平面内做半径为R的匀速圆周运动,已知重力加速度为g,空气阻力不计,则( )| A. | 若盒子在最高点时,盒子与小球之间恰好无作用力,则该盒子做匀速圆周运动的周期一定小于2π$\sqrt{\frac{R}{g}}$ | |
| B. | 盒子在最低点时盒子与小球之间的作用力一定大于2mg | |
| C. | 盒子从最低点向最高点做匀速圆周运动的过程中,球处于超重状态 | |
| D. | 若盒子以速度2$\sqrt{Rg}$做匀速圆周运动则当盒子运动到图示球心与O点位于同一水平面位置时,小球对盒子右侧面的力为4mg |
12. 中国航天局在2015年年底发射了高分四号卫星,这是中国首颗地球同步轨道高分辨率对地观测卫星,如图所示,A是静止在赤道上随地球自转的物体,B、C是同在赤道平面内的两颗人造卫星,B位于离地高度等于地球半径的圆形轨道上,C是高分四号卫星.则下列判断正确的是( )
中国航天局在2015年年底发射了高分四号卫星,这是中国首颗地球同步轨道高分辨率对地观测卫星,如图所示,A是静止在赤道上随地球自转的物体,B、C是同在赤道平面内的两颗人造卫星,B位于离地高度等于地球半径的圆形轨道上,C是高分四号卫星.则下列判断正确的是( )
 中国航天局在2015年年底发射了高分四号卫星,这是中国首颗地球同步轨道高分辨率对地观测卫星,如图所示,A是静止在赤道上随地球自转的物体,B、C是同在赤道平面内的两颗人造卫星,B位于离地高度等于地球半径的圆形轨道上,C是高分四号卫星.则下列判断正确的是( )
中国航天局在2015年年底发射了高分四号卫星,这是中国首颗地球同步轨道高分辨率对地观测卫星,如图所示,A是静止在赤道上随地球自转的物体,B、C是同在赤道平面内的两颗人造卫星,B位于离地高度等于地球半径的圆形轨道上,C是高分四号卫星.则下列判断正确的是( )| A. | 物体A随地球自转的角速度大于卫星B的角速度 | |
| B. | 卫星B的线速度小于卫星C的线速度 | |
| C. | 物体A随地球自转的周期大于卫星C的周期 | |
| D. | 物体A随地球自转的向心加速度小于卫星C的向心加速度 |
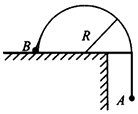 如图所示是一个横截面为半圆、半径为R的光滑柱面,一根不可伸长的细线两端分别系着物体A、B,且mA=2mB,由图示位置从静止开始释放A物体,当物体B达到圆柱顶点时,
如图所示是一个横截面为半圆、半径为R的光滑柱面,一根不可伸长的细线两端分别系着物体A、B,且mA=2mB,由图示位置从静止开始释放A物体,当物体B达到圆柱顶点时,