题目内容
5. 如图所示,两光滑且平行的固定水平杆位于同一竖直平面内,两静止小球m1、m2分别穿在两杆上,两球间连接一个保持原长的竖直轻弹簧,现给小球m2一个水平向右的初速度v0.如果两杆足够长,则在此后的运动过程中( )
如图所示,两光滑且平行的固定水平杆位于同一竖直平面内,两静止小球m1、m2分别穿在两杆上,两球间连接一个保持原长的竖直轻弹簧,现给小球m2一个水平向右的初速度v0.如果两杆足够长,则在此后的运动过程中( )| A. | m1、m2组成的系统机械能守恒 | |
| B. | 当 m1的速度达到最大时,m2同速度最小 | |
| C. | m1、m2组成的系统动量守恒 | |
| D. | 弹簧最长时,其弹性势能为$\frac{1}{2}$m2v02 |
分析 分析两球的受力情况,根据合外力是否为零判断系统动量是否守恒.对于弹簧、m1、m2组成的系统机械能守恒.弹簧最长时,m1、m2的速度相同,根据系统的动量守恒和机械能守恒列式求弹簧的弹性势能.
解答 解:A、对于弹簧、m1、m2组成的系统,只有弹力做功,系统的机械能守恒,由于弹性势能是变化的,所以m1、m2组成的系统机械能不守恒.故A错误;
B、若m1>m2,当弹簧伸长时,m1一直在加速,当弹簧再次恢复原长时m1速度达到最大.弹簧伸长时m2先减速后,速度减至零向左加速,最小速度为零.所以m1速度达到最大时,m2速度不是最小,故B错误;
C、由于两球竖直方向上受力平衡,水平方向所受的弹力的弹力大小相等,方向相反,所以两球组成的系统所受的合外力为零,系统的动量守恒,故C正确;
D、当两球的速度相等时,弹簧最长,弹簧的弹性势能最大,以向右为正方向,由动量守恒定律得:m2v0=(m1+m2)v
解得:v=$\frac{{m}_{2}{v}_{0}}{{m}_{1}+{m}_{2}}$;
由系统的机械能守恒得:$\frac{1}{2}$m2v02=$\frac{1}{2}$(m1+m2)v2+EP
解得:EP=$\frac{{m}_{1}{{m}_{2}v}_{0}^{2}}{2({m}_{1}+{m}_{2})}$,故D错误;
故选:C
点评 本题考查了动量守恒定律的应用,解决本题的关键知道两球组成的系统动量守恒,两球和弹簧组成的系统机械能守恒,分析清楚运动过程,应用动量守恒定律与机械能守恒定律即可解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.物块1、2的质量分别是m1=4kg和m2=1kg,它们具有的动能分别为E1和E2,且E1+E2=100J.若两物块沿同一直线相向运动发生碰撞,并黏在一起,欲使碰撞中损失的机械能最大,则E1和E2的值应该分别是( )
| A. | E1=E2=50 J | B. | E1=20 J,E2=80 J | C. | E1=1 J,E2=99 J | D. | E1=90 J,E2=10 J |
20. 如图所示,在0≤x≤$\sqrt{3}$a、0≤y≤a范围内有垂直于xOy平面向外的匀强磁场,磁感应强度大小为B坐标,原点O处有一个粒子源,在某时刻发射大量质量为m、电荷量为+q的带电粒子,它们的速度方向均在xOy平面的第一象限内,已知粒子在磁场中做圆周运动的周期为T,半径介于2a到3a之间,则下列说法正确的是( )
如图所示,在0≤x≤$\sqrt{3}$a、0≤y≤a范围内有垂直于xOy平面向外的匀强磁场,磁感应强度大小为B坐标,原点O处有一个粒子源,在某时刻发射大量质量为m、电荷量为+q的带电粒子,它们的速度方向均在xOy平面的第一象限内,已知粒子在磁场中做圆周运动的周期为T,半径介于2a到3a之间,则下列说法正确的是( )
 如图所示,在0≤x≤$\sqrt{3}$a、0≤y≤a范围内有垂直于xOy平面向外的匀强磁场,磁感应强度大小为B坐标,原点O处有一个粒子源,在某时刻发射大量质量为m、电荷量为+q的带电粒子,它们的速度方向均在xOy平面的第一象限内,已知粒子在磁场中做圆周运动的周期为T,半径介于2a到3a之间,则下列说法正确的是( )
如图所示,在0≤x≤$\sqrt{3}$a、0≤y≤a范围内有垂直于xOy平面向外的匀强磁场,磁感应强度大小为B坐标,原点O处有一个粒子源,在某时刻发射大量质量为m、电荷量为+q的带电粒子,它们的速度方向均在xOy平面的第一象限内,已知粒子在磁场中做圆周运动的周期为T,半径介于2a到3a之间,则下列说法正确的是( )| A. | 最后从磁场中飞出的粒子经历的时间为$\frac{T}{6}$ | |
| B. | 最后从磁场中飞出的粒子经历的时间大于$\frac{T}{6}$ | |
| C. | 最先从磁场上边界飞出的粒子经历的时间为$\frac{T}{12}$ | |
| D. | 最先从磁场上边界飞出的粒子经历的时间小于$\frac{T}{12}$ |
10.将一质量为m的木箱放在水平桌面上,现对木箱施加一斜向右下方的恒力,使木箱由静止开始以恒定的加速度a沿水平桌面向右做匀加速直线运动.已知恒力与水平方向的夹角为θ,木箱与桌面间的动摩擦因数为μ,重力加速度为g.则木箱向右运动位移x的过程中,下列说法正确的是( )
| A. | 恒力所做的功为$\frac{ma-μgx}{1+μtanθ}$ | |
| B. | 恒力所做的功为$\frac{ma+μmg}{cosθ-μsinθ}$ | |
| C. | 木箱克服摩擦力做的功为μ(mg+macos)x | |
| D. | 木箱克服摩擦力做的功为$\frac{μma-gcotθ}{cotθ-μ}x$ |
17. 如图所示,质量为 M 的楔形物体静止在光滑的水平地面上,其 斜面光滑且足够长,与水平方向的夹角为θ.一个质量为 m 的小 物块从斜面底端沿斜面向上以初速度 v0开始运动.当小物块沿斜面向上运动到最高点时,速度大小为 v,距地面高度为 h,则下列关系式中正确的是( )
如图所示,质量为 M 的楔形物体静止在光滑的水平地面上,其 斜面光滑且足够长,与水平方向的夹角为θ.一个质量为 m 的小 物块从斜面底端沿斜面向上以初速度 v0开始运动.当小物块沿斜面向上运动到最高点时,速度大小为 v,距地面高度为 h,则下列关系式中正确的是( )
 如图所示,质量为 M 的楔形物体静止在光滑的水平地面上,其 斜面光滑且足够长,与水平方向的夹角为θ.一个质量为 m 的小 物块从斜面底端沿斜面向上以初速度 v0开始运动.当小物块沿斜面向上运动到最高点时,速度大小为 v,距地面高度为 h,则下列关系式中正确的是( )
如图所示,质量为 M 的楔形物体静止在光滑的水平地面上,其 斜面光滑且足够长,与水平方向的夹角为θ.一个质量为 m 的小 物块从斜面底端沿斜面向上以初速度 v0开始运动.当小物块沿斜面向上运动到最高点时,速度大小为 v,距地面高度为 h,则下列关系式中正确的是( )| A. | mv0=(m+M )v | B. | mv0cosθ=(m+M )v | ||
| C. | mgh+$\frac{1}{2}$(m+M)v2=$\frac{1}{2}$mv02cos2θ | D. | mgh=$\frac{1}{2}$mv02-$\frac{1}{2}$mv2 |
14. 用如图所示的实验装置观察光的薄膜干涉现象.点燃酒精灯并在灯芯上洒些盐,竖立着一层肥皂液薄膜的金属丝圈.下面说法正确的是( )
用如图所示的实验装置观察光的薄膜干涉现象.点燃酒精灯并在灯芯上洒些盐,竖立着一层肥皂液薄膜的金属丝圈.下面说法正确的是( )
 用如图所示的实验装置观察光的薄膜干涉现象.点燃酒精灯并在灯芯上洒些盐,竖立着一层肥皂液薄膜的金属丝圈.下面说法正确的是( )
用如图所示的实验装置观察光的薄膜干涉现象.点燃酒精灯并在灯芯上洒些盐,竖立着一层肥皂液薄膜的金属丝圈.下面说法正确的是( )| A. | 当金属丝圈旋转30°时干涉条纹同方向旋转30° | |
| B. | 当金属丝圈旋转45°时干涉条纹同方向旋转90° | |
| C. | 当金属丝圈旋转60°时干涉条纹同方向旋转30° | |
| D. | 干涉条纹保持原来状态不变 |
15.下列说法正确的是( )
| A. | 奥斯特发现了电流的磁效应并提出了电磁感应定律 | |
| B. | 楞次发现了电流的磁效应,并研究得出了判断感应电流的方向的方法---楞次定律 | |
| C. | 发生多普勒效应时,波源的频率变化了 | |
| D. | “闻其声不见其人”是声波的衍射现象 |
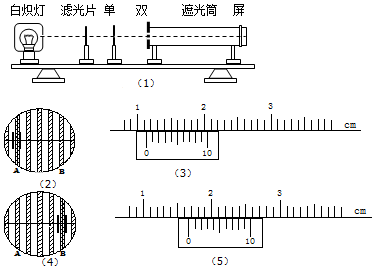 利用图中装置研究双缝干涉现象:
利用图中装置研究双缝干涉现象: