题目内容
1.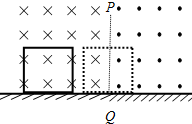 如图所示,在光滑的水平面上方,有两个磁感应强度大小均为B,方向相反的水平匀强磁场.PQ为两个磁场的边界,磁场范围足够大.一个边长为a、质量为m、电阻为R的金属正方形线框,以速度v沿垂直磁场方向从如图实线位置开始向右运动,当线框运动到分别有一半面积在两个磁场中时,线框的速度为$\frac{v}{2}$,则下列说法正确的是( )
如图所示,在光滑的水平面上方,有两个磁感应强度大小均为B,方向相反的水平匀强磁场.PQ为两个磁场的边界,磁场范围足够大.一个边长为a、质量为m、电阻为R的金属正方形线框,以速度v沿垂直磁场方向从如图实线位置开始向右运动,当线框运动到分别有一半面积在两个磁场中时,线框的速度为$\frac{v}{2}$,则下列说法正确的是( )| A. | 此时线框的加速度为$\frac{{B}^{2}{a}^{2}v}{2mR}$ | |
| B. | 此过程中通过线框截面的电量为$\frac{B{a}^{2}}{R}$ | |
| C. | 此过程中回路产生的电能为$\frac{3}{8}$mv2 | |
| D. | 此时线框中的电功率为$\frac{{{B}^{2}a}^{2}{v}^{2}}{2R}$ |
分析 线框在两个磁场中时,两条边都切割,结合切割产生的感应电动势大小,结合欧姆定律得出感应电流的大小,从而得出两条边所受安培力的合力,结合牛顿第二定律求出加速度.根据q=$n\frac{△Φ}{R}$得出此过程中通过线框截面的电量.根据能量守恒求出此回路产生的电能.结合克服安培力的功率等于电功率求出线框中的电功率.
解答 解:A、线框切割产生的感应电动势为:E=$2BL•\frac{v}{2}=BLv$,电流为:I=$\frac{E}{R}=\frac{BLv}{R}$,则安培力为:${F}_{A}=2BIL=\frac{2{B}^{2}{L}^{2}v}{R}$=$\frac{2{B}^{2}{a}^{2}v}{R}$,根据牛顿第二定律得线框的加速度为:a=$\frac{{F}_{A}}{m}=\frac{2{B}^{2}{L}^{2}v}{mR}$=$\frac{2{B}^{2}{a}^{2}v}{mR}$,故A错误.
B、根据q=$n\frac{△Φ}{R}$知,以速度v沿垂直磁场方向从如图实线位置开始向右运动,当线框运动到分别有一半面积在两个磁场中时,磁通量的变化量为:△Φ=Ba2,则此过程中通过线框截面的电量为$\frac{B{a}^{2}}{R}$,故B正确.
C、根据能量守恒定律得,此过程中产生的电能为:$E=\frac{1}{2}m{v}^{2}-\frac{1}{2}m(\frac{v}{2})^{2}=\frac{3}{8}m{v}^{2}$,故C正确.
D、此时的安培力为:${F}_{A}=2BIL=\frac{2{B}^{2}{L}^{2}v}{R}$,L=a,克服安培力的功率等于线框的电功率,则有:P=${F}_{A}\frac{v}{2}=\frac{{B}^{2}{a}^{2}{v}^{2}}{R}$,故D错误.
故选:BC.
点评 对于电磁感应问题研究思路常常有两条:一条从力的角度,重点是分析安培力作用下物体的平衡问题;另一条是能量,分析电磁感应现象中的能量如何转化是关键.在本题中,线框两条边都在切割,产生的感应电动势为两条边产生的感应电动势之和.

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 质量为m2,长度为L的小车静止在光滑水平面上,小车的左端站立着质量为m1的人.小车的右端站立着质量为m3的人,若m1>m3且两人从静止开始相向运动,互换位置,则此过程中小车的位移方向和大小为( )
质量为m2,长度为L的小车静止在光滑水平面上,小车的左端站立着质量为m1的人.小车的右端站立着质量为m3的人,若m1>m3且两人从静止开始相向运动,互换位置,则此过程中小车的位移方向和大小为( )| A. | 小车左移,位移大小为$\frac{{m}_{1}+{m}_{3}}{{m}_{1}+{m}_{2}+{m}_{3}}$L | |
| B. | 小车左移,位移大小为$\frac{{m}_{1}-m3}{{m}_{1}+{m}_{2}+{m}_{3}}$L | |
| C. | 小车右移,位移大小为$\frac{({m}_{1}+{m}_{3})-{m}_{2}}{{m}_{1}+{m}_{2}+{m}_{3}}$L | |
| D. | 小车右移,位移大小为$\frac{{m}_{2}-({m}_{1}+{m}_{3})}{{m}_{1}+{m}_{2}+{m}_{3}}$L |
| A. | 物体A的加速度大 | B. | 物体A的速度变化大 | ||
| C. | 物体B的加速度大 | D. | 物体B的速度变化大 |
| A. | E1=E2=50 J | B. | E1=20 J,E2=80 J | C. | E1=1 J,E2=99 J | D. | E1=90 J,E2=10 J |
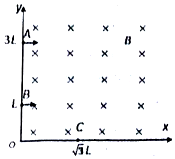 如图所示,在xOy平面的第 I象限内存在垂直xOy平面向里、磁感应强度大小为B的匀强磁场,在y轴上坐标为(0,3L)的A点和坐标为(0,L)的B点之间有若干个相同的带电粒子以相同的速度v0先后垂直于y射入磁场.由A点射入的带电粒子恰好从x轴上坐标为($\sqrt{3}$L,0)的C点射出磁场,不计粒子重力及粒子间的相互作用.则所有带电粒子离开磁场的位置在x轴上的分布范围是( )
如图所示,在xOy平面的第 I象限内存在垂直xOy平面向里、磁感应强度大小为B的匀强磁场,在y轴上坐标为(0,3L)的A点和坐标为(0,L)的B点之间有若干个相同的带电粒子以相同的速度v0先后垂直于y射入磁场.由A点射入的带电粒子恰好从x轴上坐标为($\sqrt{3}$L,0)的C点射出磁场,不计粒子重力及粒子间的相互作用.则所有带电粒子离开磁场的位置在x轴上的分布范围是( )| A. | 0≤x≤$\sqrt{3}$L | B. | $\sqrt{3}$L≤x≤2L | C. | 0≤x≤2L | D. | 2L≤x≤3L |
| A. | 恒力所做的功为$\frac{ma-μgx}{1+μtanθ}$ | |
| B. | 恒力所做的功为$\frac{ma+μmg}{cosθ-μsinθ}$ | |
| C. | 木箱克服摩擦力做的功为μ(mg+macos)x | |
| D. | 木箱克服摩擦力做的功为$\frac{μma-gcotθ}{cotθ-μ}x$ |
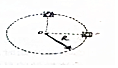 如图所示,质量为m的小球置于正方体的光滑盒子中,盒子的边长略大于球的直径.某同学拿着该盒子在竖直平面内做半径为R的匀速圆周运动,已知重力加速度为g,空气阻力不计,则( )
如图所示,质量为m的小球置于正方体的光滑盒子中,盒子的边长略大于球的直径.某同学拿着该盒子在竖直平面内做半径为R的匀速圆周运动,已知重力加速度为g,空气阻力不计,则( )| A. | 若盒子在最高点时,盒子与小球之间恰好无作用力,则该盒子做匀速圆周运动的周期一定小于2π$\sqrt{\frac{R}{g}}$ | |
| B. | 盒子在最低点时盒子与小球之间的作用力一定大于2mg | |
| C. | 盒子从最低点向最高点做匀速圆周运动的过程中,球处于超重状态 | |
| D. | 若盒子以速度2$\sqrt{Rg}$做匀速圆周运动则当盒子运动到图示球心与O点位于同一水平面位置时,小球对盒子右侧面的力为4mg |
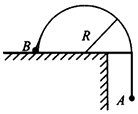 如图所示是一个横截面为半圆、半径为R的光滑柱面,一根不可伸长的细线两端分别系着物体A、B,且mA=2mB,由图示位置从静止开始释放A物体,当物体B达到圆柱顶点时,
如图所示是一个横截面为半圆、半径为R的光滑柱面,一根不可伸长的细线两端分别系着物体A、B,且mA=2mB,由图示位置从静止开始释放A物体,当物体B达到圆柱顶点时,