题目内容
3.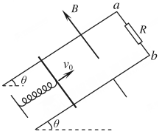 如图所示,固定的光滑金属导轨间距为L=1m,导轨电阻不计,上端a、b间接有阻值为R=1.5Ω的电阻,导轨平面与水平面的夹角为θ=30°,且处在磁感应强度大小为B=1T、方向垂直于导轨平面向上的匀强磁场中.质量为m=0.4kg、电阻为r=0.5Ω的导体棒与固定弹簧相连后放在导轨上.初始时刻,弹簧恰处于自然长度,导体棒具有沿轨道向上的初速度v0=1m/s.整个运动过程中导体棒始终与导轨垂直并保持良好接触.已知弹簧的劲度系数为k=10N/m,弹簧的中心轴线与导轨平行.
如图所示,固定的光滑金属导轨间距为L=1m,导轨电阻不计,上端a、b间接有阻值为R=1.5Ω的电阻,导轨平面与水平面的夹角为θ=30°,且处在磁感应强度大小为B=1T、方向垂直于导轨平面向上的匀强磁场中.质量为m=0.4kg、电阻为r=0.5Ω的导体棒与固定弹簧相连后放在导轨上.初始时刻,弹簧恰处于自然长度,导体棒具有沿轨道向上的初速度v0=1m/s.整个运动过程中导体棒始终与导轨垂直并保持良好接触.已知弹簧的劲度系数为k=10N/m,弹簧的中心轴线与导轨平行.(1)求初始时刻通过电阻R的电流I的大小和方向;
(2)当导体棒第一次回到初始位置时,速度变为v=0.8m/s,求此时导体棒的加速度大小a;
(3)导体棒最终静止时弹簧的弹性势能为Ep=0.2J,求导体棒从开始运动直到停止的过程中,电阻R上产生的焦耳热Q.
分析 (1)根据切割产生的感应电动势公式求出初始时刻的电动势,结合闭合电路欧姆定律求出电流的大小,根据右手定则得出感应电流的方向.
(2)根据切割产生的感应电动势公式、安培力公式和欧姆定律得出速度为v时的安培力,结合牛顿第二定律求出导体棒的加速度.
(3)导体棒最终静止时处于压缩状态,根据胡克定律以及平衡求出压缩量,结合能量守恒求出整个回路产生的热量,从而得出电阻R上产生的热量.
解答 解:(1)初始时刻,棒产生的感应电动势为:E1=BLv0=1×1×1V=1V,
则通过电阻的电流为:${I}_{1}=\frac{E}{R+r}=\frac{1}{1.5+0.5}A=0.5A$,根据右手定则知,通过电阻R的电流方向由b到a.
(2)第一次回到初始位置所受的安培力为:${F}_{A}=BIL=\frac{{B}^{2}{L}^{2}v}{R+r}$,
根据牛顿第二定律得加速度为:a=$\frac{mgsinθ-{F}_{A}}{m}=gsinθ-\frac{{B}^{2}{L}^{2}v}{R+r}$=10×0.5-$\frac{1×1×0.8}{0.4×2}$=4m/s2.
(3)导体棒最终静止时有:mgsinθ=kx,
解得压缩量为:x=$\frac{mgsinθ}{k}$,
设整个过程回路产生的焦耳热为Q,根据能量守恒有:$\frac{1}{2}m{{v}_{0}}^{2}+mgxsinθ={E}_{p}+{Q}_{总}$,
则${Q}_{总}=\frac{1}{2}m{{v}_{0}}^{2}+\frac{(mgsinθ)^{2}}{k}-{E}_{p}$,
电阻R上产生的热量为:Q=$\frac{R}{R+r}{Q}_{总}$,
代入数据解得:Q=0.3J.
答:(1)初始时刻通过电阻R的电流的大小为0.5A,通过电阻R的电流方向由b到a.
(2)此时导体棒的加速度大小为4m/s2;
(3)导体棒从开始运动直到停止的过程中,电阻R上产生的焦耳热为0.3J.
点评 解决本题的关键会根据牛顿第二定律求加速度,以及结合运动学能够分析出金属棒的运动情况,注意动能定理求出的热量,并不是金属棒的热量,而是金属棒与内阻共有的.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案| A. | 匀加速直线运动,匀变速曲线运动 | B. | 匀加速直线运动,匀减速直线运动 | ||
| C. | 匀变速曲线运动,匀速圆周运动 | D. | 匀加速直线运动,匀速圆周运动 |
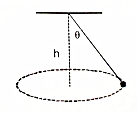 如图所示,圆锥摆的摆球质量为m,摆球悬挂点到轨迹圆的圆心的距离为h,当摆球以某一线速度在水平面内做匀速圆周运动时,摆线与竖直方向的夹角为θ,若不计空气阻力的影响,重力加速度为g,则下面有关判断中正确的是( )
如图所示,圆锥摆的摆球质量为m,摆球悬挂点到轨迹圆的圆心的距离为h,当摆球以某一线速度在水平面内做匀速圆周运动时,摆线与竖直方向的夹角为θ,若不计空气阻力的影响,重力加速度为g,则下面有关判断中正确的是( )| A. | 摆线上的张力大小等于mgcosθ | B. | 摆球的向心力大小等于mgtanθ | ||
| C. | 摆球的线速度大小等于$\sqrt{ghtanθ}$ | D. | 摆球的周期等于2π$\sqrt{\frac{h}{g}}$ |
 轻绳一端固定在光滑轴O上,另一端系一质量为m的小球,在最低点给小球一初速度v0,使其在竖直平面内做圆周运动,且恰好能通过最高点P(不计空气阻力).下列说法正确的是( )
轻绳一端固定在光滑轴O上,另一端系一质量为m的小球,在最低点给小球一初速度v0,使其在竖直平面内做圆周运动,且恰好能通过最高点P(不计空气阻力).下列说法正确的是( )| A. | 小球在最低点时对绳的拉力大小为mg | |
| B. | 小球在最高点时对绳的拉力大小为mg | |
| C. | 若增大小球的初速度,则过最高点时球对绳的力一定增大 | |
| D. | 若增大小球的初速度,则在最低点时球对绳的力不一定增大 |

| A. | 甲和乙 | B. | 乙和丙 | C. | 丙和丁 | D. | 甲和丁 |
 如图相距为L的两光滑平行导轨,平行放置在倾角为θ的斜面上,导轨的右端接有电阻R(轨道电阻不计),斜面处在一匀强磁场B中,磁场方向垂直于斜面向上,质量为m,电阻为R的金属棒ab放在导轨上,与导轨接触良好,由静止释放,下滑距离s后速度最大,则( )
如图相距为L的两光滑平行导轨,平行放置在倾角为θ的斜面上,导轨的右端接有电阻R(轨道电阻不计),斜面处在一匀强磁场B中,磁场方向垂直于斜面向上,质量为m,电阻为R的金属棒ab放在导轨上,与导轨接触良好,由静止释放,下滑距离s后速度最大,则( )| A. | 下滑过程电阻R消耗的最大功率为$\frac{{m}^{2}{g}^{2}si{n}^{2}θ}{{B}^{2}{L}^{2}}$R | |
| B. | 下滑过程电阻R消耗的最大功率为$\frac{3{m}^{2}{g}^{2}si{n}^{2}θ}{{B}^{2}{L}^{2}}$R | |
| C. | 下滑过程重力做功为mgssinθ | |
| D. | 下滑过程克服安培力做的功为$\frac{9{m}^{3}{g}^{2}si{n}^{2}θ}{2{B}^{4}{L}^{4}}$R2 |
 如图所示,用粗细相同的铜丝做成边长分别为L和3L的两只闭合线框a和b,现将两线框分别以va、vb的速度从磁感应强度为B的匀强磁场区域中匀速地拉到磁场外,若va=2vb,则在此过程中外力对线框做的功分别为Wa、Wb,通过两导体框某一截面的电量分别为Qa、Qb,则( )
如图所示,用粗细相同的铜丝做成边长分别为L和3L的两只闭合线框a和b,现将两线框分别以va、vb的速度从磁感应强度为B的匀强磁场区域中匀速地拉到磁场外,若va=2vb,则在此过程中外力对线框做的功分别为Wa、Wb,通过两导体框某一截面的电量分别为Qa、Qb,则( )| A. | Wa:Wb=2:27 | B. | Wa:Wb=2:9 | C. | Qa、Qb=1:9 | D. | Qa、Qb=1:3 |

