题目内容
2. 轻绳一端固定在光滑轴O上,另一端系一质量为m的小球,在最低点给小球一初速度v0,使其在竖直平面内做圆周运动,且恰好能通过最高点P(不计空气阻力).下列说法正确的是( )
轻绳一端固定在光滑轴O上,另一端系一质量为m的小球,在最低点给小球一初速度v0,使其在竖直平面内做圆周运动,且恰好能通过最高点P(不计空气阻力).下列说法正确的是( )| A. | 小球在最低点时对绳的拉力大小为mg | |
| B. | 小球在最高点时对绳的拉力大小为mg | |
| C. | 若增大小球的初速度,则过最高点时球对绳的力一定增大 | |
| D. | 若增大小球的初速度,则在最低点时球对绳的力不一定增大 |
分析 抓住小球恰好能够通过最高点P,结合绳子的拉力为零求出最高点的速度,根据动能定理求出最低点的速度,再结合牛顿第二定律求出最低点绳子的拉力.当小球的速度变化时,根据牛顿第二定律分析绳子拉力的变化.
解答 解:A、小球恰好能通过最高点,可知小球在最高点时,绳子的拉力为零,根据牛顿第二定律得,$mg=m\frac{{v}^{2}}{L}$,解得最高点的速度v=$\sqrt{gL}$,根据动能定理得,$mg•2L=\frac{1}{2}m{{v}_{0}}^{2}-\frac{1}{2}m{v}^{2}$,解得${v}_{0}=\sqrt{5gL}$,在最低点,根据牛顿第二定律得,$F-mg=m\frac{{{v}_{0}}^{2}}{L}$,解得绳子的拉力F=6mg,故A、B错误.
C、若增大小球的初速度,则小球通过最高点的速度增大,根据$F′+mg=m\frac{{v}^{2}}{L}$知,在最高点球对绳子的拉力一定增大,故C正确.
D、在最低点,根据$F-mg=m\frac{{{v}_{0}}^{2}}{L}$知,若增大初速度,则绳子的拉力一定增大,故D错误.
故选:C.
点评 解决本题的关键知道小球做圆周运动向心力的来源,结合牛顿第二定律进行求解,难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 超级电容器又叫双电层电容器,是一种新型储能装置.它具有功率密度高、充放电时间短、循环寿命长、工作温度范围宽等特点.如图为一款超级电容器,其标有“3V,3000F”,则可知( )
超级电容器又叫双电层电容器,是一种新型储能装置.它具有功率密度高、充放电时间短、循环寿命长、工作温度范围宽等特点.如图为一款超级电容器,其标有“3V,3000F”,则可知( )
 超级电容器又叫双电层电容器,是一种新型储能装置.它具有功率密度高、充放电时间短、循环寿命长、工作温度范围宽等特点.如图为一款超级电容器,其标有“3V,3000F”,则可知( )
超级电容器又叫双电层电容器,是一种新型储能装置.它具有功率密度高、充放电时间短、循环寿命长、工作温度范围宽等特点.如图为一款超级电容器,其标有“3V,3000F”,则可知( )| A. | 电压为0时,该电容器的电容为0 | |
| B. | 电压为2V时,该电容器的电容为2000F | |
| C. | 该电容器正常工作时的电荷量为9000C | |
| D. | 该电容器正常工作时的电荷量为1000C |
10.验证机械能守恒定律的方法很多,落体法验证机械能守恒定律就是其中的一种,图示是利用透明直尺自由下落和光电计时器来验证机械能守恒定律的简易示意图.当有不透光的物体从光电门间通过时,光电计时器就可以显示物体的挡光时间,所用的光电门传感器可测得最短时间为0.01ms.将挡光效果好、宽度d=3.8×10-3m的黑色磁带贴在透明直尺上,现将直尺从一定高度由静止释放,并使其竖直通过光电门.一同学测得各段黑色磁带通过光电门的时间△ti与图中所示的高度差△hi,并将部分数据进行了处理,结果如图所示.(取g=9.8m/s2,表格中M=0.1kg为直尺的质量)
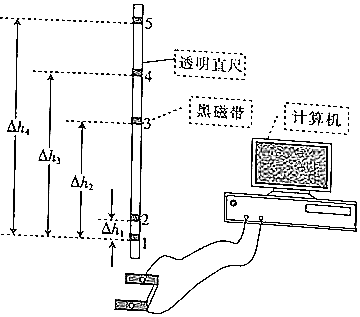
(1)从表格中的数据可知,直尺上磁带通过光电门的瞬时速度是利用vi=$\frac{d}{△{t}_{i}}$求出的,请你简要分析该同学这样做的理由是:当位移很小,时间很短时可以利用平均速度来代替瞬时速度,由于本题中挡光物的尺寸很小,挡光时间很短,因此直尺上磁带通过光电门的瞬时速度可以利用vi=$\frac{d}{△{t}_{i}}$求出.
(2)表格中的数据①、②、③分别为4.22m/s、0.397J、0.402J.
(3)通过实验得出的结论是:在实验误差允许的范围内,机械能守恒.
(4)根据该实验,请你判断下列△Ek-△h图象中正确的是C.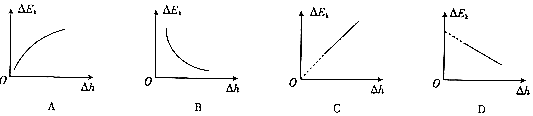

| △ti(×10-3s) | vi=$\frac{d}{△{t}_{i}}$(m/s) | △Eki=$\frac{1}{2}$Mv${\;}_{i}^{2}$$-\frac{1}{2}$Mv${\;}_{1}^{2}$(J) | △hi(m) | Mghi(J) | |
| 1 | 1.21 | 3.14 | - | - | - |
| 2 | 1.15 | 3.30 | 0.052 | 0.06 | 0.059 |
| 3 | 1.00 | 3.80 | 0.229 | 0.24 | 0.235 |
| 4 | 0.95 | 4.00 | 0.307 | 0.32 | 0.314 |
| 5 | 0.90 | ① | ② | 0.41 | ③ |
(2)表格中的数据①、②、③分别为4.22m/s、0.397J、0.402J.
(3)通过实验得出的结论是:在实验误差允许的范围内,机械能守恒.
(4)根据该实验,请你判断下列△Ek-△h图象中正确的是C.

7. 如图所示,先后使一矩形线圈以速度v1和v2匀速通过有界匀强磁场区域,已知v1=2v2,在先后两种情况下( )
如图所示,先后使一矩形线圈以速度v1和v2匀速通过有界匀强磁场区域,已知v1=2v2,在先后两种情况下( )
 如图所示,先后使一矩形线圈以速度v1和v2匀速通过有界匀强磁场区域,已知v1=2v2,在先后两种情况下( )
如图所示,先后使一矩形线圈以速度v1和v2匀速通过有界匀强磁场区域,已知v1=2v2,在先后两种情况下( )| A. | 通过线圈某截面的电荷量之比q1:q2=1:1 | |
| B. | 线圈中的感应电动势之比为E1:E2=2:1 | |
| C. | 线圈中的感应电流之比为I1:I2=2:1 | |
| D. | 线圈中产生的焦耳热之比为Q1:Q2=1:4 |
8.一小型宇宙飞船沿人造地球卫星的轨道在高空中做匀速圆周运动时,在飞船上沿与飞船运动的相反方向抛出一个质量不可忽略的小物体P,则下列说法中正确的有( )
| A. | 飞船一定离开原来轨道运动 | B. | P一定离开原来轨道运动 | ||
| C. | 火箭运动半径一定增大 | D. | P运动半径一定减小 |
 利用如图所示的装置可以探究系统机械能守恒,在滑块B上安装宽度为L(较小)的遮光板(遮光板质量忽略不计),把滑块B放在水平放置的气垫导轨上,通过跨过定滑轮的绳与钩码A相连,连接好光电门与数字毫秒计,两光电门间距离用S表示.数字毫秒计能够记录滑块先后通过两个光电门的时间△t1、△t2,当地的重力加速度为g.请分析回答下列问题
利用如图所示的装置可以探究系统机械能守恒,在滑块B上安装宽度为L(较小)的遮光板(遮光板质量忽略不计),把滑块B放在水平放置的气垫导轨上,通过跨过定滑轮的绳与钩码A相连,连接好光电门与数字毫秒计,两光电门间距离用S表示.数字毫秒计能够记录滑块先后通过两个光电门的时间△t1、△t2,当地的重力加速度为g.请分析回答下列问题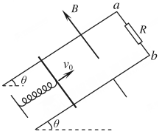 如图所示,固定的光滑金属导轨间距为L=1m,导轨电阻不计,上端a、b间接有阻值为R=1.5Ω的电阻,导轨平面与水平面的夹角为θ=30°,且处在磁感应强度大小为B=1T、方向垂直于导轨平面向上的匀强磁场中.质量为m=0.4kg、电阻为r=0.5Ω的导体棒与固定弹簧相连后放在导轨上.初始时刻,弹簧恰处于自然长度,导体棒具有沿轨道向上的初速度v0=1m/s.整个运动过程中导体棒始终与导轨垂直并保持良好接触.已知弹簧的劲度系数为k=10N/m,弹簧的中心轴线与导轨平行.
如图所示,固定的光滑金属导轨间距为L=1m,导轨电阻不计,上端a、b间接有阻值为R=1.5Ω的电阻,导轨平面与水平面的夹角为θ=30°,且处在磁感应强度大小为B=1T、方向垂直于导轨平面向上的匀强磁场中.质量为m=0.4kg、电阻为r=0.5Ω的导体棒与固定弹簧相连后放在导轨上.初始时刻,弹簧恰处于自然长度,导体棒具有沿轨道向上的初速度v0=1m/s.整个运动过程中导体棒始终与导轨垂直并保持良好接触.已知弹簧的劲度系数为k=10N/m,弹簧的中心轴线与导轨平行.