题目内容
15.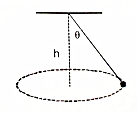 如图所示,圆锥摆的摆球质量为m,摆球悬挂点到轨迹圆的圆心的距离为h,当摆球以某一线速度在水平面内做匀速圆周运动时,摆线与竖直方向的夹角为θ,若不计空气阻力的影响,重力加速度为g,则下面有关判断中正确的是( )
如图所示,圆锥摆的摆球质量为m,摆球悬挂点到轨迹圆的圆心的距离为h,当摆球以某一线速度在水平面内做匀速圆周运动时,摆线与竖直方向的夹角为θ,若不计空气阻力的影响,重力加速度为g,则下面有关判断中正确的是( )| A. | 摆线上的张力大小等于mgcosθ | B. | 摆球的向心力大小等于mgtanθ | ||
| C. | 摆球的线速度大小等于$\sqrt{ghtanθ}$ | D. | 摆球的周期等于2π$\sqrt{\frac{h}{g}}$ |
分析 小球受绳子的张力和重力两个力作用,靠两个力的合力提供向心力,结合平行四边形定则求出摆线的张力以及向心力大小,根据牛顿第二定律求出摆球的线速度和周期.
解答  解:A、摆球的受力如图所示,根据平行四边形定则知,摆线的张力T=$\frac{mg}{cosθ}$,故A错误.
解:A、摆球的受力如图所示,根据平行四边形定则知,摆线的张力T=$\frac{mg}{cosθ}$,故A错误.
B、根据平行四边形定则知,摆球的向心力Fn=mgtanθ,故B正确.
C、根据牛顿第二定律得,$mgtanθ=m\frac{{v}^{2}}{Lsinθ}$,解得摆球的线速度v=$\sqrt{gLtanθsinθ}$,故C错误.
D、根据牛顿第二定律得,$mgtanθ=mr\frac{4{π}^{2}}{{T}^{2}}$,解得摆球的周期T=$2π\sqrt{\frac{Lcosθ}{g}}=2π\sqrt{\frac{h}{g}}$,故D正确.
故选:BD.
点评 该题是一个圆锥摆模型,对于圆周摆,在竖直方向上受力平衡,在水平方向上的合力提供向心力,结合向心力公式求解.

练习册系列答案
相关题目
5.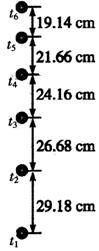 某同学利用频闪照相法验证机械能守恒定律.该同学将一质量为m=0.2kg的小球竖直上抛,获得部分运动过程的频闪照片如图所示.已知图中所标数据为实际距离,频闪仪每隔0.05s闪光一次,当地重力加速度为10m/s2.该同学通过计算得到不同时刻的速度如下表:
某同学利用频闪照相法验证机械能守恒定律.该同学将一质量为m=0.2kg的小球竖直上抛,获得部分运动过程的频闪照片如图所示.已知图中所标数据为实际距离,频闪仪每隔0.05s闪光一次,当地重力加速度为10m/s2.该同学通过计算得到不同时刻的速度如下表:
(1)根据频闪照片上的数据计算t5时刻小球的速度v5=4.08m/s;
(2)从t2时刻到t5时刻,小球重力势能的增加量△Ep=1.45J,动能的减少量△Ek=1.46J. 在误差允许的范围内,若△Ep与△Ek近似相等,就能验证机械能守恒定律.(以上结果均保留三位有效数字)
 某同学利用频闪照相法验证机械能守恒定律.该同学将一质量为m=0.2kg的小球竖直上抛,获得部分运动过程的频闪照片如图所示.已知图中所标数据为实际距离,频闪仪每隔0.05s闪光一次,当地重力加速度为10m/s2.该同学通过计算得到不同时刻的速度如下表:
某同学利用频闪照相法验证机械能守恒定律.该同学将一质量为m=0.2kg的小球竖直上抛,获得部分运动过程的频闪照片如图所示.已知图中所标数据为实际距离,频闪仪每隔0.05s闪光一次,当地重力加速度为10m/s2.该同学通过计算得到不同时刻的速度如下表:| 时刻 | t2 | t3 | t4 | t5 |
| 速度(m/s) | 5.59 | 5.08 | 4.58 |
(2)从t2时刻到t5时刻,小球重力势能的增加量△Ep=1.45J,动能的减少量△Ek=1.46J. 在误差允许的范围内,若△Ep与△Ek近似相等,就能验证机械能守恒定律.(以上结果均保留三位有效数字)
10.验证机械能守恒定律的方法很多,落体法验证机械能守恒定律就是其中的一种,图示是利用透明直尺自由下落和光电计时器来验证机械能守恒定律的简易示意图.当有不透光的物体从光电门间通过时,光电计时器就可以显示物体的挡光时间,所用的光电门传感器可测得最短时间为0.01ms.将挡光效果好、宽度d=3.8×10-3m的黑色磁带贴在透明直尺上,现将直尺从一定高度由静止释放,并使其竖直通过光电门.一同学测得各段黑色磁带通过光电门的时间△ti与图中所示的高度差△hi,并将部分数据进行了处理,结果如图所示.(取g=9.8m/s2,表格中M=0.1kg为直尺的质量)
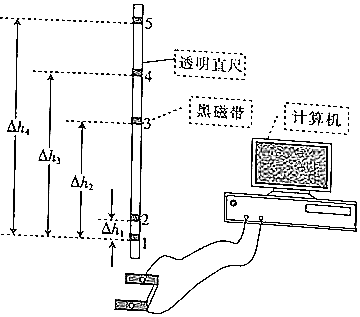
(1)从表格中的数据可知,直尺上磁带通过光电门的瞬时速度是利用vi=$\frac{d}{△{t}_{i}}$求出的,请你简要分析该同学这样做的理由是:当位移很小,时间很短时可以利用平均速度来代替瞬时速度,由于本题中挡光物的尺寸很小,挡光时间很短,因此直尺上磁带通过光电门的瞬时速度可以利用vi=$\frac{d}{△{t}_{i}}$求出.
(2)表格中的数据①、②、③分别为4.22m/s、0.397J、0.402J.
(3)通过实验得出的结论是:在实验误差允许的范围内,机械能守恒.
(4)根据该实验,请你判断下列△Ek-△h图象中正确的是C.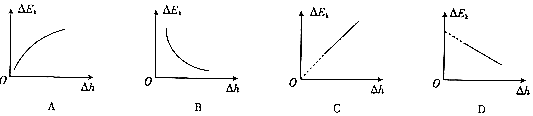

| △ti(×10-3s) | vi=$\frac{d}{△{t}_{i}}$(m/s) | △Eki=$\frac{1}{2}$Mv${\;}_{i}^{2}$$-\frac{1}{2}$Mv${\;}_{1}^{2}$(J) | △hi(m) | Mghi(J) | |
| 1 | 1.21 | 3.14 | - | - | - |
| 2 | 1.15 | 3.30 | 0.052 | 0.06 | 0.059 |
| 3 | 1.00 | 3.80 | 0.229 | 0.24 | 0.235 |
| 4 | 0.95 | 4.00 | 0.307 | 0.32 | 0.314 |
| 5 | 0.90 | ① | ② | 0.41 | ③ |
(2)表格中的数据①、②、③分别为4.22m/s、0.397J、0.402J.
(3)通过实验得出的结论是:在实验误差允许的范围内,机械能守恒.
(4)根据该实验,请你判断下列△Ek-△h图象中正确的是C.

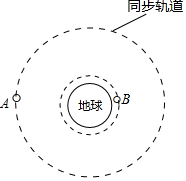 如图所示,A是地球同步卫星,B是近地卫星,它们的轨道半径之比为6:1
如图所示,A是地球同步卫星,B是近地卫星,它们的轨道半径之比为6:1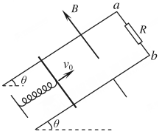 如图所示,固定的光滑金属导轨间距为L=1m,导轨电阻不计,上端a、b间接有阻值为R=1.5Ω的电阻,导轨平面与水平面的夹角为θ=30°,且处在磁感应强度大小为B=1T、方向垂直于导轨平面向上的匀强磁场中.质量为m=0.4kg、电阻为r=0.5Ω的导体棒与固定弹簧相连后放在导轨上.初始时刻,弹簧恰处于自然长度,导体棒具有沿轨道向上的初速度v0=1m/s.整个运动过程中导体棒始终与导轨垂直并保持良好接触.已知弹簧的劲度系数为k=10N/m,弹簧的中心轴线与导轨平行.
如图所示,固定的光滑金属导轨间距为L=1m,导轨电阻不计,上端a、b间接有阻值为R=1.5Ω的电阻,导轨平面与水平面的夹角为θ=30°,且处在磁感应强度大小为B=1T、方向垂直于导轨平面向上的匀强磁场中.质量为m=0.4kg、电阻为r=0.5Ω的导体棒与固定弹簧相连后放在导轨上.初始时刻,弹簧恰处于自然长度,导体棒具有沿轨道向上的初速度v0=1m/s.整个运动过程中导体棒始终与导轨垂直并保持良好接触.已知弹簧的劲度系数为k=10N/m,弹簧的中心轴线与导轨平行.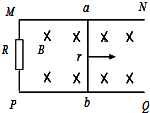 图中磁场的磁感应强度B=1T,平行导轨宽L=1m,R=1Ω,金属棒ab以1m/s的速度紧贴导轨向右运动,其他电阻不计,试求通过R的电流大小和方向.
图中磁场的磁感应强度B=1T,平行导轨宽L=1m,R=1Ω,金属棒ab以1m/s的速度紧贴导轨向右运动,其他电阻不计,试求通过R的电流大小和方向.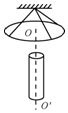 如图所示,用三角细线悬挂的水平圆形线圈共有n匝,线圈由粗细均匀、单位长度的质量为2.5g的导线绕制而成,三条细线呈对称分布,稳定时线圈平面水平.在线圈正下方放有一个圆柱形条形磁铁,磁铁的中轴线OO'垂直于线圈平面且通过其圆心O,测得线圈的导线所在处磁感应强度大小为0.5T,方向与竖直线成30°角,要使三条细线上的张力为零,则条形磁铁上端为S极,线圈中通过的电流至少为0.1A(线圈的电流方向俯视为逆时针).
如图所示,用三角细线悬挂的水平圆形线圈共有n匝,线圈由粗细均匀、单位长度的质量为2.5g的导线绕制而成,三条细线呈对称分布,稳定时线圈平面水平.在线圈正下方放有一个圆柱形条形磁铁,磁铁的中轴线OO'垂直于线圈平面且通过其圆心O,测得线圈的导线所在处磁感应强度大小为0.5T,方向与竖直线成30°角,要使三条细线上的张力为零,则条形磁铁上端为S极,线圈中通过的电流至少为0.1A(线圈的电流方向俯视为逆时针).