题目内容
12. 如图所示,用粗细相同的铜丝做成边长分别为L和3L的两只闭合线框a和b,现将两线框分别以va、vb的速度从磁感应强度为B的匀强磁场区域中匀速地拉到磁场外,若va=2vb,则在此过程中外力对线框做的功分别为Wa、Wb,通过两导体框某一截面的电量分别为Qa、Qb,则( )
如图所示,用粗细相同的铜丝做成边长分别为L和3L的两只闭合线框a和b,现将两线框分别以va、vb的速度从磁感应强度为B的匀强磁场区域中匀速地拉到磁场外,若va=2vb,则在此过程中外力对线框做的功分别为Wa、Wb,通过两导体框某一截面的电量分别为Qa、Qb,则( )| A. | Wa:Wb=2:27 | B. | Wa:Wb=2:9 | C. | Qa、Qb=1:9 | D. | Qa、Qb=1:3 |
分析 将闭合线框a和b匀速拉出磁场,根据功能关系可知,外力对环做的功等于线框产生的焦耳热.根据感应电动势公式、焦耳定律、电阻定律研究功的关系.由法拉第电磁感应定律求出感应电动势,由欧姆定律求出电流,由电流定义式求出电荷量,然后求出电荷量之比.
解答 解:A、切割产生的感应电动势E=BLv,电流I=$\frac{E}{R}=\frac{BLv}{R}$,安培力${F}_{A}=BIL=\frac{{B}^{2}{L}^{2}v}{R}$,拉力等于安培力,则外力对线框做功W=FL=$\frac{{B}^{2}{L}^{3}v}{R}$,又R=$ρ\frac{4L}{S}$,解得W=$\frac{{B}^{2}{L}^{2}vS}{4ρ}$,因为速度之比为2:1,边长之比为1:3,则Wa:Wb=2:9,故A错误,B正确.
C、通过横截面的电量Q=$\overline{I}△t=\frac{△Φ}{△tR}△t=\frac{△Φ}{R}=\frac{B{L}^{2}}{ρ\frac{4L}{S}}$=$\frac{BLS}{4ρ}$,因为边长之比为1:3,则Qa:Qb=1:3,故C错误,D正确.
故选:BD.
点评 本题综合了感应电动势、焦耳定律、电阻定律,关键根据功能关系得到外力对环做的功的表达式,运用比例法进行分析.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
7. 如图所示,先后使一矩形线圈以速度v1和v2匀速通过有界匀强磁场区域,已知v1=2v2,在先后两种情况下( )
如图所示,先后使一矩形线圈以速度v1和v2匀速通过有界匀强磁场区域,已知v1=2v2,在先后两种情况下( )
 如图所示,先后使一矩形线圈以速度v1和v2匀速通过有界匀强磁场区域,已知v1=2v2,在先后两种情况下( )
如图所示,先后使一矩形线圈以速度v1和v2匀速通过有界匀强磁场区域,已知v1=2v2,在先后两种情况下( )| A. | 通过线圈某截面的电荷量之比q1:q2=1:1 | |
| B. | 线圈中的感应电动势之比为E1:E2=2:1 | |
| C. | 线圈中的感应电流之比为I1:I2=2:1 | |
| D. | 线圈中产生的焦耳热之比为Q1:Q2=1:4 |
17.把一只矩形线圈从匀强磁场中匀速拉出.第一次用速度v1,第二次用速度v2,且v2=2v1.若两次拉力所做的功分别为W1和W2,两次做功的功率分别为P1和P2,两次线圈产生的热量为Q1和Q2,通过导线截面的电荷量为q1和q2则下述结论正确的是( )
| A. | W1=W2,P1=P2 | B. | W2=2W1,P2=4P1 | C. | Q2=2Q1,q1= q2 | D. | Q2=Q1,2q1=q2 |
2.关于光的波粒二象性及物质波,下列说法正确的是( )
| A. | 光子的动量和波长成反比 | |
| B. | 康普顿效应说明光具有波动性 | |
| C. | 光的波粒二象性说明,光的波动性明显时,粒子性也一定明显 | |
| D. | 电子显微镜利用电子束达到微小物体表面,再反射到荧光板上成像来实现观察,这是由于电子束的德布罗意波长较长 |
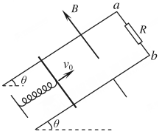 如图所示,固定的光滑金属导轨间距为L=1m,导轨电阻不计,上端a、b间接有阻值为R=1.5Ω的电阻,导轨平面与水平面的夹角为θ=30°,且处在磁感应强度大小为B=1T、方向垂直于导轨平面向上的匀强磁场中.质量为m=0.4kg、电阻为r=0.5Ω的导体棒与固定弹簧相连后放在导轨上.初始时刻,弹簧恰处于自然长度,导体棒具有沿轨道向上的初速度v0=1m/s.整个运动过程中导体棒始终与导轨垂直并保持良好接触.已知弹簧的劲度系数为k=10N/m,弹簧的中心轴线与导轨平行.
如图所示,固定的光滑金属导轨间距为L=1m,导轨电阻不计,上端a、b间接有阻值为R=1.5Ω的电阻,导轨平面与水平面的夹角为θ=30°,且处在磁感应强度大小为B=1T、方向垂直于导轨平面向上的匀强磁场中.质量为m=0.4kg、电阻为r=0.5Ω的导体棒与固定弹簧相连后放在导轨上.初始时刻,弹簧恰处于自然长度,导体棒具有沿轨道向上的初速度v0=1m/s.整个运动过程中导体棒始终与导轨垂直并保持良好接触.已知弹簧的劲度系数为k=10N/m,弹簧的中心轴线与导轨平行.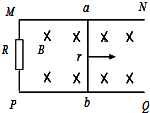 图中磁场的磁感应强度B=1T,平行导轨宽L=1m,R=1Ω,金属棒ab以1m/s的速度紧贴导轨向右运动,其他电阻不计,试求通过R的电流大小和方向.
图中磁场的磁感应强度B=1T,平行导轨宽L=1m,R=1Ω,金属棒ab以1m/s的速度紧贴导轨向右运动,其他电阻不计,试求通过R的电流大小和方向. 如图所示,正方形单匝均匀线框abcd,边长L=0.4m,每边电阻相等,总电阻R=0.5Ω.一根足够长的绝缘轻质细线跨过两个轻质光滑定滑轮,一端连接正方形线框,另一端连接绝缘物体P,物体P放在一个光滑的足够长的固定斜面上,斜面倾角θ=30°,斜面上方的细线与斜面平行.在正方形线框正下方有一有界的匀强磁场,上边界I和下边界II都水平,两边界之间距离也是L=0.4m.磁场方向水平,垂直纸面向里,磁感应强度大小B=0.5T.现让正方形线框的cd边距上边界I的正上方高度h=0.9m的位置由静止释放,且线框在运动过程中始终与磁场垂直,cd边始终保持水平,物体P始终在斜面上运动,线框刚好能以v=3m/s的速度进入匀强磁场并匀速通过匀强磁场区域.释放前细线绷紧,重力加速度 g=10m/s2,不计空气阻力.
如图所示,正方形单匝均匀线框abcd,边长L=0.4m,每边电阻相等,总电阻R=0.5Ω.一根足够长的绝缘轻质细线跨过两个轻质光滑定滑轮,一端连接正方形线框,另一端连接绝缘物体P,物体P放在一个光滑的足够长的固定斜面上,斜面倾角θ=30°,斜面上方的细线与斜面平行.在正方形线框正下方有一有界的匀强磁场,上边界I和下边界II都水平,两边界之间距离也是L=0.4m.磁场方向水平,垂直纸面向里,磁感应强度大小B=0.5T.现让正方形线框的cd边距上边界I的正上方高度h=0.9m的位置由静止释放,且线框在运动过程中始终与磁场垂直,cd边始终保持水平,物体P始终在斜面上运动,线框刚好能以v=3m/s的速度进入匀强磁场并匀速通过匀强磁场区域.释放前细线绷紧,重力加速度 g=10m/s2,不计空气阻力.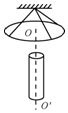 如图所示,用三角细线悬挂的水平圆形线圈共有n匝,线圈由粗细均匀、单位长度的质量为2.5g的导线绕制而成,三条细线呈对称分布,稳定时线圈平面水平.在线圈正下方放有一个圆柱形条形磁铁,磁铁的中轴线OO'垂直于线圈平面且通过其圆心O,测得线圈的导线所在处磁感应强度大小为0.5T,方向与竖直线成30°角,要使三条细线上的张力为零,则条形磁铁上端为S极,线圈中通过的电流至少为0.1A(线圈的电流方向俯视为逆时针).
如图所示,用三角细线悬挂的水平圆形线圈共有n匝,线圈由粗细均匀、单位长度的质量为2.5g的导线绕制而成,三条细线呈对称分布,稳定时线圈平面水平.在线圈正下方放有一个圆柱形条形磁铁,磁铁的中轴线OO'垂直于线圈平面且通过其圆心O,测得线圈的导线所在处磁感应强度大小为0.5T,方向与竖直线成30°角,要使三条细线上的张力为零,则条形磁铁上端为S极,线圈中通过的电流至少为0.1A(线圈的电流方向俯视为逆时针).