题目内容
15.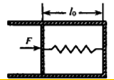 如图所示,内壁光滑的圆柱形导热气缸固定在水平面上,气缸内被活塞封有一定质量的理想气体,活塞横截面积为S,质量和厚度都不计,活塞通过弹簧与气缸底部连接在一起,弹簧处于原长,已知周围环境温度为T0,大气压强恒为p0,弹簧的劲度系数k=$\frac{{p}_{0}S}{{l}_{0}}$(S为活塞横截面积),原长为l0,一段时间后,环境温度降低,在活塞上施加一水平向右的压力,使活塞缓慢向右移动,当压力增大到某一值时保持恒定,此时活塞向右移动了0.2l0,缸内气体压强为1.1p0.
如图所示,内壁光滑的圆柱形导热气缸固定在水平面上,气缸内被活塞封有一定质量的理想气体,活塞横截面积为S,质量和厚度都不计,活塞通过弹簧与气缸底部连接在一起,弹簧处于原长,已知周围环境温度为T0,大气压强恒为p0,弹簧的劲度系数k=$\frac{{p}_{0}S}{{l}_{0}}$(S为活塞横截面积),原长为l0,一段时间后,环境温度降低,在活塞上施加一水平向右的压力,使活塞缓慢向右移动,当压力增大到某一值时保持恒定,此时活塞向右移动了0.2l0,缸内气体压强为1.1p0.(1)求此时缸内气体的温度T1;
(2)对气缸加热,使气体温度缓慢升高,当活塞移动到距气缸底部1.2l0时,求此时缸内气体的温度T2.
分析 (1)根据理想气体状态方程求缸内气体的温度
(2)根据理想气体状态方程和对活塞受力平衡联立求解
解答 解:(1)汽缸内的气体,初态时:压强为${p}_{0}^{\;}$,体积为${V}_{0}^{\;}=S{l}_{0}^{\;}$,温度为${T}_{0}^{\;}$
末态时:压强为${p}_{1}^{\;}=1.1{p}_{0}^{\;}$,体积为${V}_{1}^{\;}=S(l-0.2{l}_{0}^{\;})$
由理想气体状态方程得:
$\frac{{p}_{0}^{\;}{V}_{0}^{\;}}{{T}_{0}^{\;}}=\frac{{p}_{1}^{\;}{V}_{1}^{\;}}{{T}_{1}^{\;}}$
解得:${T}_{1}^{\;}=0.88{T}_{0}^{\;}$
(2)当活塞移动到距气缸底部$1.2{l}_{0}^{\;}$时,体积为${V}_{2}^{\;}=1.2S{l}_{0}^{\;}$,设气体压强为${p}_{2}^{\;}$,
由理想气体状态方程得:
$\frac{{p}_{0}^{\;}{V}_{0}^{\;}}{{T}_{0}^{\;}}=\frac{{p}_{2}^{\;}{V}_{2}^{\;}}{{T}_{2}^{\;}}$
此时活塞受力平衡方程为:
${p}_{0}^{\;}S+F-{p}_{2}^{\;}S+k(1.2{l}_{0}^{\;}-{l}_{0}^{\;})=0$
当活塞向右移动$0.2{l}_{0}^{\;}$后压力F保持恒定,活塞受力平衡
${p}_{0}^{\;}S+F-1.1{p}_{0}^{\;}S-k(0,2{l}_{0}^{\;})=0$
解得:${T}_{2}^{\;}=1.8{T}_{0}^{\;}$
答:(1)求此时缸内气体的温度${T}_{1}^{\;}$为$0.88{T}_{0}^{\;}$;
(2)对气缸加热,使气体温度缓慢升高,当活塞移动到距气缸底部1.2l0时,求此时缸内气体的温度${T}_{2}^{\;}$为$1.8{T}_{0}^{\;}$.
点评 本题考查了理想气体状态方程的应用,根据平衡条件求出气体的压强是正确解题的关键,根据题意求出气体的初末状态参量,应用理想气体状态方程即可正确解题.

 阅读快车系列答案
阅读快车系列答案| A. | 甲、乙两恒星的线速度之比$\sqrt{3}$:$\sqrt{2}$ | |
| B. | 甲、乙两恒星的加速度之比为2:3 | |
| C. | 甲、乙两恒星的线速度之比为3:2 | |
| D. | 甲、乙两恒星的向心加速度之比为2:3 |
| A. | 地球绕太阳公转的周期T和地球中心到太阳中心的距离r | |
| B. | 月球绕地球转动的周期T和月球球心到地球球心的距离r | |
| C. | 地球表面的重力加速度g和地球的半径R | |
| D. | 同步卫星的轨道半径r |
| A. | 天宫一号在轨正常运行时的速度大小为$\sqrt{\frac{g{R}^{2}}{R+H}}$ | |
| B. | 终止服务后,在P点应增大天宫一号的速度,使其轨道降低 | |
| C. | 下降过程中由于气体阻力做负功,天宫一号的动能会减小 | |
| D. | 下降过程中即使不干预,天宫一号的动能也会增加 |
 如图所示为氦原子(He+)的能级示意图,大量处在n=4的激发态的He+,在向较低能级跃迁的过程中向外发出光子,并用这些光照射逸出功为3.34eV的锌板.
如图所示为氦原子(He+)的能级示意图,大量处在n=4的激发态的He+,在向较低能级跃迁的过程中向外发出光子,并用这些光照射逸出功为3.34eV的锌板.