题目内容
3.有两颗人造卫星,都绕地球做匀速圆周运行,已知它们的轨道半径之比r1:r2=9:4.对于这两颗卫星的运动,求:(1)线速度之比;
(2)周期之比;
(3)向心加速度之比.
分析 (1)人造卫星绕地球做匀速圆周运行所需的向心力来源于万有引力,根据牛顿第二定律列式可得线速度与半径的关系.
(2)由T=$\frac{2πr}{v}$可得周期之比;
(3)由a=$\frac{{v}^{2}}{r}$可得向心加速度之比.
解答 解:(1)万有引力提供向心力,由牛顿第二定律可得:
$G\frac{Mm}{r}=m\frac{{v}^{2}}{r}$,解得v=$\sqrt{\frac{GM}{r}}$
轨道半径之比r1:r2=9:4,所以线速度之比:v1:v2=2:3;
(2)由T=$\frac{2πr}{v}$知,周期之比T1:T2=$\frac{{r}_{1}}{{r}_{2}}•\frac{{v}_{2}}{{v}_{1}}$=$\frac{9}{4}×\frac{3}{2}$=27:8;
(3)由a=$\frac{{v}^{2}}{r}$知,向心加速度之比a1:a2=$\frac{{v}_{1}^{2}}{{v}_{2}^{2}}•\frac{{r}_{2}}{{r}_{1}}$=$\frac{4}{9}×\frac{4}{9}$=16:81.
答:(1)线速度之比为2:3;
(2)周期之比为27:8;
(3)向心加速度之比为16:81.
点评 解题的关键是要知道天体的运动所需的向心力完全来源于万有引力,根据牛顿第二定律和向心力公式求解.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
18. 在匀强磁场中有一个静止的氡原子核(${\;}_{86}^{222}$Rn),由于衰变它放出一个粒子,此粒子的径迹与反冲核的径迹是两个相外切的圆,大圆与小圆的直径之比为42:1,如图所示.那么氡核的衰变方程应是下列方程中的哪一个( )
在匀强磁场中有一个静止的氡原子核(${\;}_{86}^{222}$Rn),由于衰变它放出一个粒子,此粒子的径迹与反冲核的径迹是两个相外切的圆,大圆与小圆的直径之比为42:1,如图所示.那么氡核的衰变方程应是下列方程中的哪一个( )
 在匀强磁场中有一个静止的氡原子核(${\;}_{86}^{222}$Rn),由于衰变它放出一个粒子,此粒子的径迹与反冲核的径迹是两个相外切的圆,大圆与小圆的直径之比为42:1,如图所示.那么氡核的衰变方程应是下列方程中的哪一个( )
在匀强磁场中有一个静止的氡原子核(${\;}_{86}^{222}$Rn),由于衰变它放出一个粒子,此粒子的径迹与反冲核的径迹是两个相外切的圆,大圆与小圆的直径之比为42:1,如图所示.那么氡核的衰变方程应是下列方程中的哪一个( )| A. | ${\;}_{86}^{222}$Rn→${\;}_{87}^{222}$Fr+${\;}_{-1}^{0}$e | B. | ${\;}_{86}^{222}$Rn→${\;}_{84}^{218}$Po+${\;}_{2}^{4}$He | ||
| C. | ${\;}_{86}^{222}$Rn→${\;}_{85}^{222}$At+${\;}_{1}^{0}$e | D. | ${\;}_{86}^{222}$Rn→${\;}_{85}^{220}$At+${\;}_{1}^{2}$H |
8. 如图,一矩形线圈的面积为S,匝数为N,电阻为r,处于磁感应强度大小为B的水平匀强磁场中,绕垂直磁场的水平轴OO′以角速度ω匀速转动.线圈通过滑环与定电阻R及理想电流表团合回路.已知理想电压表的示数为U,从线圈平面与磁感线平行的位置开始计时.则( )
如图,一矩形线圈的面积为S,匝数为N,电阻为r,处于磁感应强度大小为B的水平匀强磁场中,绕垂直磁场的水平轴OO′以角速度ω匀速转动.线圈通过滑环与定电阻R及理想电流表团合回路.已知理想电压表的示数为U,从线圈平面与磁感线平行的位置开始计时.则( )
 如图,一矩形线圈的面积为S,匝数为N,电阻为r,处于磁感应强度大小为B的水平匀强磁场中,绕垂直磁场的水平轴OO′以角速度ω匀速转动.线圈通过滑环与定电阻R及理想电流表团合回路.已知理想电压表的示数为U,从线圈平面与磁感线平行的位置开始计时.则( )
如图,一矩形线圈的面积为S,匝数为N,电阻为r,处于磁感应强度大小为B的水平匀强磁场中,绕垂直磁场的水平轴OO′以角速度ω匀速转动.线圈通过滑环与定电阻R及理想电流表团合回路.已知理想电压表的示数为U,从线圈平面与磁感线平行的位置开始计时.则( )| A. | R两端电压瞬时值的表达式为uR=$\sqrt{2}$Usinωt | |
| B. | 理想电流表的示数为$\frac{\sqrt{2}NBSω}{2(R+r)}$ | |
| C. | 从$\frac{π}{2ω}$到$\frac{3π}{2ω}$的时间内,穿过线圈平面磁通量的变化量为零 | |
| D. | 若ω=100πrad/s,通过R的电流表每秒钟方向改变50次 |
12.下面关于机械波的说法,正确的是( )
| A. | 波的产生需要两个条件,即波源和传播波的介质 | |
| B. | 波动过程是质点由近及远的传递过程 | |
| C. | 波动过程中质点不可能发生沿波传播方向上的迁移 | |
| D. | 波动过程是能量传递的过程 |
 某学习小组利用功能关系结合图象法求解出了弹性势能的表达式为Ep=$\frac{1}{2}k{x}^{2}$.其中x为弹簧的形变量,k为弹簧的劲度系数.学习小组为了验证此表达式是否正确,设计如图甲所示的实验装置:将劲度系数为k的轻质弹簧左端固定.再将一小球与弹簧右端接触但不拴连,然后向左推小球,使弹簧压缩一段距离后将小球由静止释放,小球向右运动一段距离后脱离桌面落在水平地面上,遁过测量和计算可以验证弹性势能的表达式是否正确.已知重力加速度为g,忽略所有阻力.
某学习小组利用功能关系结合图象法求解出了弹性势能的表达式为Ep=$\frac{1}{2}k{x}^{2}$.其中x为弹簧的形变量,k为弹簧的劲度系数.学习小组为了验证此表达式是否正确,设计如图甲所示的实验装置:将劲度系数为k的轻质弹簧左端固定.再将一小球与弹簧右端接触但不拴连,然后向左推小球,使弹簧压缩一段距离后将小球由静止释放,小球向右运动一段距离后脱离桌面落在水平地面上,遁过测量和计算可以验证弹性势能的表达式是否正确.已知重力加速度为g,忽略所有阻力. 在一墙面上用绳栓一质量为10kg的小球,现给它一个10m/s的初速度,让其在水平面上以R=5m的半径做匀速圆周运动,具体情况见图.求:在小球运动的过程中,绳对小球有多大的拉力?
在一墙面上用绳栓一质量为10kg的小球,现给它一个10m/s的初速度,让其在水平面上以R=5m的半径做匀速圆周运动,具体情况见图.求:在小球运动的过程中,绳对小球有多大的拉力?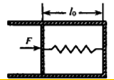 如图所示,内壁光滑的圆柱形导热气缸固定在水平面上,气缸内被活塞封有一定质量的理想气体,活塞横截面积为S,质量和厚度都不计,活塞通过弹簧与气缸底部连接在一起,弹簧处于原长,已知周围环境温度为T0,大气压强恒为p0,弹簧的劲度系数k=$\frac{{p}_{0}S}{{l}_{0}}$(S为活塞横截面积),原长为l0,一段时间后,环境温度降低,在活塞上施加一水平向右的压力,使活塞缓慢向右移动,当压力增大到某一值时保持恒定,此时活塞向右移动了0.2l0,缸内气体压强为1.1p0.
如图所示,内壁光滑的圆柱形导热气缸固定在水平面上,气缸内被活塞封有一定质量的理想气体,活塞横截面积为S,质量和厚度都不计,活塞通过弹簧与气缸底部连接在一起,弹簧处于原长,已知周围环境温度为T0,大气压强恒为p0,弹簧的劲度系数k=$\frac{{p}_{0}S}{{l}_{0}}$(S为活塞横截面积),原长为l0,一段时间后,环境温度降低,在活塞上施加一水平向右的压力,使活塞缓慢向右移动,当压力增大到某一值时保持恒定,此时活塞向右移动了0.2l0,缸内气体压强为1.1p0.