题目内容
5.甲、乙两双星相距为L,质量之比M甲:M乙=2:3,它们离其他天体都很遥远,我们观察到它们的距离始终保持不变,由此可知( )| A. | 甲、乙两恒星的线速度之比$\sqrt{3}$:$\sqrt{2}$ | |
| B. | 甲、乙两恒星的加速度之比为2:3 | |
| C. | 甲、乙两恒星的线速度之比为3:2 | |
| D. | 甲、乙两恒星的向心加速度之比为2:3 |
分析 甲、乙两恒星的距离始终保持不变,靠相互间的万有引力提供向心力,具有相同的角速度.根据万有引力定律和向心力公式求解线速度之比和向心加速度之比.
解答 解:据题可知甲、乙两恒星的距离始终保持不变,围绕两星连线上的一点做匀速圆周运动,靠相互间的万有引力提供向心力,角速度一定相同.双星靠相互间的万有引力提供向心力,角速度大小相等,向心力大小相等,则有:$G\frac{{M}_{甲}^{\;}{M}_{乙}^{\;}}{{L}_{\;}^{2}}={M}_{甲}^{\;}{ω}_{\;}^{2}{r}_{甲}^{\;}={M}_{乙}^{\;}{ω}_{\;}^{2}{r}_{乙}^{\;}$
则有${M}_{甲}^{\;}{r}_{甲}^{\;}={M}_{乙}^{\;}{r}_{乙}^{\;}$
$\frac{{r}_{甲}^{\;}}{{r}_{乙}^{\;}}=\frac{{M}_{乙}^{\;}}{{M}_{甲}^{\;}}=\frac{3}{2}$
根据v=ωr得$\frac{{v}_{甲}^{\;}}{{v}_{乙}^{\;}}=\frac{{r}_{甲}^{\;}}{{r}_{乙}^{\;}}=\frac{3}{2}$,故AB错误
根据$a={ω}_{\;}^{2}r$得$\frac{{a}_{甲}^{\;}}{{a}_{乙}^{\;}}=\frac{{r}_{甲}^{\;}}{{r}_{乙}^{\;}}=\frac{3}{2}$,故C正确,D错误
故选:C
点评 解决本题的关键知道双星系统的特点,角速度大小相等,向心力大小相等,再根据万有引力定律和圆周运动规律结合解答.

练习册系列答案
相关题目
10. 用一条绝缘轻绳悬挂一个带电小球,小球质量为1.0×10-2kg,所带电荷量为2.0×10-8C.现加一水平方向的匀强电场,平衡时绝缘绳与铅垂线成45°角(g=10m/s2),下列说法正确的是( )
用一条绝缘轻绳悬挂一个带电小球,小球质量为1.0×10-2kg,所带电荷量为2.0×10-8C.现加一水平方向的匀强电场,平衡时绝缘绳与铅垂线成45°角(g=10m/s2),下列说法正确的是( )
 用一条绝缘轻绳悬挂一个带电小球,小球质量为1.0×10-2kg,所带电荷量为2.0×10-8C.现加一水平方向的匀强电场,平衡时绝缘绳与铅垂线成45°角(g=10m/s2),下列说法正确的是( )
用一条绝缘轻绳悬挂一个带电小球,小球质量为1.0×10-2kg,所带电荷量为2.0×10-8C.现加一水平方向的匀强电场,平衡时绝缘绳与铅垂线成45°角(g=10m/s2),下列说法正确的是( )| A. | 匀强电场水平向右 | |
| B. | 这个匀强电场的电场强度大小为5×106N/C | |
| C. | 将轻绳拉至竖直位置,小球也会处于平衡状态 | |
| D. | 将轻绳拉离初始位置,小球会做往复运动 |
15.如图所示,小球从距地面高度为2R的斜面上P点无初速度释放,分别滑上甲、乙、丙、丁四个轨道,甲为半径为1.2R的半圆轨道,乙为半径为2R的$\frac{1}{4}$圆轨道、轨道和地面连接处有一段小圆弧,丙为半径为R的半圆轨道,丁为高为l.5R的斜面、斜面和地面连接处有一段小圆弧,所有接触面均光滑,则滑上四个轨道后运动到的最高点能和P等高的是( )


| A. | 甲 | B. | 乙 | C. | 乙和丙 | D. | 甲、乙、丙、丁 |
17. 2016年3月8日天文爱好者迎来了“土星冲日”的美丽天象,“土星冲日”是指土星和太阳正好分处地球的两侧,二者几乎成一条直线.该天象每399天发生一次,土星和地球绕太阳公转的方向相同,公转轨迹都近似为圆,根据我们日常生活知识可知( )
2016年3月8日天文爱好者迎来了“土星冲日”的美丽天象,“土星冲日”是指土星和太阳正好分处地球的两侧,二者几乎成一条直线.该天象每399天发生一次,土星和地球绕太阳公转的方向相同,公转轨迹都近似为圆,根据我们日常生活知识可知( )
 2016年3月8日天文爱好者迎来了“土星冲日”的美丽天象,“土星冲日”是指土星和太阳正好分处地球的两侧,二者几乎成一条直线.该天象每399天发生一次,土星和地球绕太阳公转的方向相同,公转轨迹都近似为圆,根据我们日常生活知识可知( )
2016年3月8日天文爱好者迎来了“土星冲日”的美丽天象,“土星冲日”是指土星和太阳正好分处地球的两侧,二者几乎成一条直线.该天象每399天发生一次,土星和地球绕太阳公转的方向相同,公转轨迹都近似为圆,根据我们日常生活知识可知( )| A. | 土星公转的速率比地球大 | |
| B. | 土星公转的周期为399天 | |
| C. | 土星公转的向心加速度比地球小 | |
| D. | 假如土星适度加速,有可能与地球实现对接 |
 如图所示,固定的圆弧轨道与水平面平滑连接,轨道与水平面均光滑,质量为m的物块B与轻质弹簧拴接静止在水平面上,弹簧右端固定.质量为3m的物块A从圆弧轨道上距离水平面高h处由静止释放,与B碰撞后推着B一起运动但与B不粘连.求:
如图所示,固定的圆弧轨道与水平面平滑连接,轨道与水平面均光滑,质量为m的物块B与轻质弹簧拴接静止在水平面上,弹簧右端固定.质量为3m的物块A从圆弧轨道上距离水平面高h处由静止释放,与B碰撞后推着B一起运动但与B不粘连.求: 某学习小组利用功能关系结合图象法求解出了弹性势能的表达式为Ep=$\frac{1}{2}k{x}^{2}$.其中x为弹簧的形变量,k为弹簧的劲度系数.学习小组为了验证此表达式是否正确,设计如图甲所示的实验装置:将劲度系数为k的轻质弹簧左端固定.再将一小球与弹簧右端接触但不拴连,然后向左推小球,使弹簧压缩一段距离后将小球由静止释放,小球向右运动一段距离后脱离桌面落在水平地面上,遁过测量和计算可以验证弹性势能的表达式是否正确.已知重力加速度为g,忽略所有阻力.
某学习小组利用功能关系结合图象法求解出了弹性势能的表达式为Ep=$\frac{1}{2}k{x}^{2}$.其中x为弹簧的形变量,k为弹簧的劲度系数.学习小组为了验证此表达式是否正确,设计如图甲所示的实验装置:将劲度系数为k的轻质弹簧左端固定.再将一小球与弹簧右端接触但不拴连,然后向左推小球,使弹簧压缩一段距离后将小球由静止释放,小球向右运动一段距离后脱离桌面落在水平地面上,遁过测量和计算可以验证弹性势能的表达式是否正确.已知重力加速度为g,忽略所有阻力.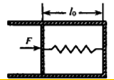 如图所示,内壁光滑的圆柱形导热气缸固定在水平面上,气缸内被活塞封有一定质量的理想气体,活塞横截面积为S,质量和厚度都不计,活塞通过弹簧与气缸底部连接在一起,弹簧处于原长,已知周围环境温度为T0,大气压强恒为p0,弹簧的劲度系数k=$\frac{{p}_{0}S}{{l}_{0}}$(S为活塞横截面积),原长为l0,一段时间后,环境温度降低,在活塞上施加一水平向右的压力,使活塞缓慢向右移动,当压力增大到某一值时保持恒定,此时活塞向右移动了0.2l0,缸内气体压强为1.1p0.
如图所示,内壁光滑的圆柱形导热气缸固定在水平面上,气缸内被活塞封有一定质量的理想气体,活塞横截面积为S,质量和厚度都不计,活塞通过弹簧与气缸底部连接在一起,弹簧处于原长,已知周围环境温度为T0,大气压强恒为p0,弹簧的劲度系数k=$\frac{{p}_{0}S}{{l}_{0}}$(S为活塞横截面积),原长为l0,一段时间后,环境温度降低,在活塞上施加一水平向右的压力,使活塞缓慢向右移动,当压力增大到某一值时保持恒定,此时活塞向右移动了0.2l0,缸内气体压强为1.1p0.