16.已知抛物线y2=2px(p>0),过点C(-4,0)作抛物线的两条切线CA,CB,A,B为切点,若直线AB经过抛物线y2=2px的焦点,△CAB的面积为24,则以直线AB为准线的抛物线标准方程是( )
| A. | y2=4x | B. | y2=-4x | C. | y2=8x | D. | y2=-8x |
15.大厦一层有A,B,C,D四部电梯,3人在一层乘坐电梯上楼,则其中2人恰好乘坐同一部电梯的概率为( )
| A. | $\frac{9}{16}$ | B. | $\frac{7}{16}$ | C. | $\frac{9}{32}$ | D. | $\frac{7}{32}$ |
14.已知等差数列{an},S3=6,a9+a11+a13=60,则S13的值为( )
| A. | 66 | B. | 42 | C. | 169 | D. | 156 |
11.某程序框图如图所示,运行该程序输出的k值是( )
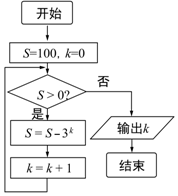

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
10.某几何体的三视图如图所示,则该几何体的表面积为( )


| A. | 8(π+4) | B. | 8(π+8) | C. | 16(π+4) | D. | 16(π+8) |
9.已知集合A={x|x2-x<0},B={x|x<a},若A∩B=A,则实数a的取值范围是( )
| A. | (-∞,1] | B. | (-∞,1) | C. | [1,+∞) | D. | (1,+∞) |
8. 某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如表(假设该区域空气质量指数不会超过300):
某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如表(假设该区域空气质量指数不会超过300):
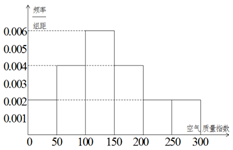
该社团将该校区在2016年100天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.
(Ⅰ)请估算2017年(以365天计算)全年空气质量优良的天数(未满一天按一天计算);
(Ⅱ)用分层抽样的方法共抽取10天,则空气质量指数在(0,50],(50,100],(100,150]的天数中各应抽取几天?
(Ⅲ)已知空气质量等级为1级时不需要净化空气,空气质量等级为2级时每天需净化空气的费用为2000元,空气质量等级为3级时每天需净化空气的费用为4000元.若在(Ⅱ)的条件下,从空气质量指数在(0,150]的天数中任意抽取两天,求这两天的净化空气总费用为4000元的概率.
0 240241 240249 240255 240259 240265 240267 240271 240277 240279 240285 240291 240295 240297 240301 240307 240309 240315 240319 240321 240325 240327 240331 240333 240335 240336 240337 240339 240340 240341 240343 240345 240349 240351 240355 240357 240361 240367 240369 240375 240379 240381 240385 240391 240397 240399 240405 240409 240411 240417 240421 240427 240435 266669
 某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如表(假设该区域空气质量指数不会超过300):
某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如表(假设该区域空气质量指数不会超过300):| 空气质量指数 | (0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] |
| 空气质量等级 | 1级优 | 2级良 | 3级轻度 污染 | 4级中度 污染 | 5级重度 污染 | 6级严重污染 |
(Ⅰ)请估算2017年(以365天计算)全年空气质量优良的天数(未满一天按一天计算);
(Ⅱ)用分层抽样的方法共抽取10天,则空气质量指数在(0,50],(50,100],(100,150]的天数中各应抽取几天?
(Ⅲ)已知空气质量等级为1级时不需要净化空气,空气质量等级为2级时每天需净化空气的费用为2000元,空气质量等级为3级时每天需净化空气的费用为4000元.若在(Ⅱ)的条件下,从空气质量指数在(0,150]的天数中任意抽取两天,求这两天的净化空气总费用为4000元的概率.