15．
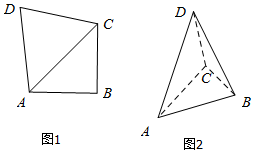如图，在四边形ABCD中，AB=BC=2，∠ABC=90°，DA=DC=$\sqrt{6}$．现沿对角线AC折起，使得平面DAC⊥平面ABC，此时点A，B，C，D在同一个球面上，则该球的体积是（ ）
如图，在四边形ABCD中，AB=BC=2，∠ABC=90°，DA=DC=$\sqrt{6}$．现沿对角线AC折起，使得平面DAC⊥平面ABC，此时点A，B，C，D在同一个球面上，则该球的体积是（ ）| A． | $\frac{9}{2}π$ | B． | $\frac{{8\sqrt{2}}}{3}π$ | C． | $\frac{27}{2}π$ | D． | 12π |
如图，水平放置的△ABC的斜二测直观图是图中的△A′B′C′，已知A′C′=6，B′C′=4，则AB边的实际长度是（ ）
13．为迎接春节，某工厂大批生产小孩具--拼图，工厂为了规定工时定额，需要确定加工拼图所花费的时间，为此进行了10次试验，测得的数据如下：
（1）画出散点图，并判断y与x是否具有线性相关关系；
（2）求回归方程；
（3）根据求出的回归方程，预测加工2010个拼图需要用多少小时？（精确到0.1）
附：回归直线的斜率和截距的最小二乘估计公式分别为：$\hat b=\frac{{\sum_{i=1}^n{（{x_i}-\bar x）（{y_i}-\bar y}）}}{{\sum_{i=1}^n{{{（{x_i}-\bar x）}^2}}}}$$，\hat a=\bar y-\hat b\bar x$．
| 拼图数x/个 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| 加工时间y/分钟 | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 |
（2）求回归方程；
（3）根据求出的回归方程，预测加工2010个拼图需要用多少小时？（精确到0.1）
附：回归直线的斜率和截距的最小二乘估计公式分别为：$\hat b=\frac{{\sum_{i=1}^n{（{x_i}-\bar x）（{y_i}-\bar y}）}}{{\sum_{i=1}^n{{{（{x_i}-\bar x）}^2}}}}$$，\hat a=\bar y-\hat b\bar x$．
| 参考数据 | 合计 | ||||||||||
| x | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 550 |
| y | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 | 917 |
| xi2 | 100 | 400 | 900 | 1600 | 2500 | 3600 | 4900 | 6400 | 8100 | 10000 | 38500 |
| xiyi | 620 | 1360 | 2250 | 3240 | 4450 | 5700 | 7140 | 8840 | 10350 | 12200 | 55950 |
9．
《算法统宗》是中国古代数学名著，由明代数学家程大位所著，该著作完善了珠算口诀，确立了算盘用法，完成了由筹算到珠算的彻底转变，对我国民间普及珠算和数学知识起到了很大的作用．如图所示的程序框图的算法思路源于该著作中的“李白沽酒”问题，执行该程序框图，若输入的a值为$\frac{93}{32}$，则输出的m的值为（ ）
《算法统宗》是中国古代数学名著，由明代数学家程大位所著，该著作完善了珠算口诀，确立了算盘用法，完成了由筹算到珠算的彻底转变，对我国民间普及珠算和数学知识起到了很大的作用．如图所示的程序框图的算法思路源于该著作中的“李白沽酒”问题，执行该程序框图，若输入的a值为$\frac{93}{32}$，则输出的m的值为（ ）| A． | $\frac{9}{4}$ | B． | $\frac{3}{2}$ | C． | 0 | D． | -3 |
7．已知$\frac{a}{c^2}$＞$\frac{b}{c^2}$，则下列不等式一定成立的是（ ）
0 240116 240124 240130 240134 240140 240142 240146 240152 240154 240160 240166 240170 240172 240176 240182 240184 240190 240194 240196 240200 240202 240206 240208 240210 240211 240212 240214 240215 240216 240218 240220 240224 240226 240230 240232 240236 240242 240244 240250 240254 240256 240260 240266 240272 240274 240280 240284 240286 240292 240296 240302 240310 266669
| A． | a2＞b2 | B． | $\frac{1}{b}$＞$\frac{1}{a}$ | C． | lg a＞lg b | D． | （$\frac{1}{3}$）b＞（$\frac{1}{3}$）a |