题目内容
15.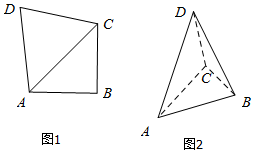 如图,在四边形ABCD中,AB=BC=2,∠ABC=90°,DA=DC=$\sqrt{6}$.现沿对角线AC折起,使得平面DAC⊥平面ABC,此时点A,B,C,D在同一个球面上,则该球的体积是( )
如图,在四边形ABCD中,AB=BC=2,∠ABC=90°,DA=DC=$\sqrt{6}$.现沿对角线AC折起,使得平面DAC⊥平面ABC,此时点A,B,C,D在同一个球面上,则该球的体积是( )| A. | $\frac{9}{2}π$ | B. | $\frac{{8\sqrt{2}}}{3}π$ | C. | $\frac{27}{2}π$ | D. | 12π |
分析 根据两平面的形状寻找外球球的球心位置,利用勾股定理求出外接球半径,从而可得出球的体积.
解答 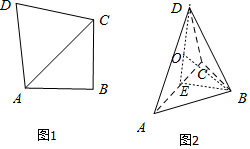 解:在图2中,取AC的中点E,连结DE,BE,
解:在图2中,取AC的中点E,连结DE,BE,
∵AD=CD,∴DE⊥AC,
∵平面ACD∩平面ABC=AC,平面ACD⊥平面ABC,
DE?平面ACD,
∴DE⊥平面ABC,
∵∠ABC=90°,
∴棱锥外接球的球心O在直线DE上,
∵AD=CD=$\sqrt{6}$,AB=BC=2,∠ABC=90°,
∴BE=AE=CE=$\frac{1}{2}$AC=$\sqrt{2}$,DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=2,
设OE=x,则OD=2-x,OB=$\sqrt{B{E}^{2}+O{E}^{2}}$=$\sqrt{{x}^{2}+2}$,
∴2-x=$\sqrt{{x}^{2}+2}$,解得x=$\frac{1}{2}$,
∴外接球的半径r=2-x=$\frac{3}{2}$,
∴外接球的体积V=$\frac{4π{r}^{3}}{3}$=$\frac{4π}{3}$×($\frac{3}{2}$)3=$\frac{9π}{2}$.
故选A.
点评 本题考查了棱锥与外接球的位置关系,球的体积计算,属于中档题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
5.已知平面内一点p∈{(x,y)|(x-2cosθ)2+(y-2sinθ) 2=16,θ∈R},则满足条件的点P在平面内所组成的图形的面积是( )
| A. | 8π | B. | 16π | C. | 24π | D. | 32π |
6.2017年5月14日至15日,中国在北京举办“一带一路”国际合作高峰论坛,与其它60多个成员国共商大计.设S是由不少于4个成员国代表组成的集合,如果S中任意4个代表都至少有1个人与另外3个人认识,那么下列判定正确的是( )
| A. | S中没有人认识S中所有的人 | B. | S中至少有1人认识S中所有的人 | ||
| C. | S中至多有2人不认识S中所有的人 | D. | S中至多有2人认识S中所有的人 |
3.下列各式正确的是( )
| A. | arctan(-1)=$\frac{3π}{4}$ | B. | arctan($\frac{1}{2}$)=$\frac{π}{6}$ | C. | arcsin(-$\frac{1}{2}$)=-$\frac{π}{6}$ | D. | arccos(-$\frac{1}{2}$)=-$\frac{π}{3}$ |
20.定义在R上的函数f(x)满足:①f(-x)=-f(x);②f(2x)=af(x)(a>0);③当2≤x≤4时,$f(x)=|sin\frac{π}{2}x|$,若分别以函数f(x)的极值点和相应极值为横、纵坐标的点都在一条直线上,则a的值为( )
| A. | 1 | B. | 2 | C. | 1或2 | D. | 2或3 |
7.化简$C_n^0-2C_n^1+{2^2}C_n^2+…+{(-1)^n}{2^n}C_n^n$=( )
| A. | 1 | B. | -1 | C. | (-1)n | D. | (-1)n-1 |
5.执行如图的程序框图,输出S的值是( )


| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | -1 |