13.如图所示给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图,其中判断框内应填入的条件是( )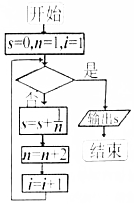

| A. | i>1010 | B. | i<1010 | C. | i>1009 | D. | i<1009 |
12.复平面上平行四边形ABCD的四个顶点中,A、B、C所对应的复数分别为2-3i、-2-3i、-3+2i,则D点对应的复数是( )
| A. | 1+2i | B. | 1-2i | C. | 2-i | D. | 2+i |
9.已知定认在R上的可导函数f(x)的导函数f′(x),若对于任意实数x,有f′(x)<f(x),且y=f(x)-1为奇函数,则不等式f(x)<ex的解集为( )
| A. | (0,+∞) | B. | (-∞,0) | C. | (-∞,e4) | D. | (e4,+∞) |
8.4个不同的小球全部随意放入3个不同的盒子里,使每个盒子都不空的放法种数为( )
| A. | C${\;}_{4}^{1}$C${\;}_{4}^{3}$C${\;}_{2}^{2}$ | B. | A${\;}_{3}^{1}$A${\;}_{4}^{3}$ | ||
| C. | C${\;}_{4}^{3}$A${\;}_{2}^{2}$ | D. | ${C}_{4}^{2}{A}_{3}^{3}$ |
7.下面几种推理中是演绎推理的为( )
| A. | 科学家利用鱼的沉浮原理制造潜艇 | |
| B. | 猜想数列$\frac{1}{1×2}$,$\frac{1}{2×3}$,$\frac{1}{3×4}$,…的通项公式为an=$\frac{1}{n(n+1)}$(n∈N+) | |
| C. | 半径为r的圆的面积S=πr2,则单位圆的面积S=π | |
| D. | 由平面直角坐标系中圆的方程为(x-a)2+(y-b)2=r2,推测空间直角坐标系中球的方程为(x-a)2+(y-b)2+(z-c)2=r2 |
6.下列求导运算正确的是( )
| A. | (log2x)′=$\frac{1}{xln2}$ | B. | ($\frac{cosx}{x}$)′=$\frac{xsinx-cosx}{x}$ | ||
| C. | (10x)′=10xlge | D. | (x+$\sqrt{x}$)′=1-$\frac{1}{2\sqrt{x}}$ |
4.已知某海滨浴场的海浪高度(单位:米)是时间(单位:小时,0≤t≤24)的函数,记作y=f(t),如表是某日各时的浪高数据:
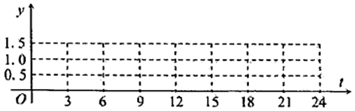
(Ⅰ)在如图的网格中描出所给的点;
(Ⅱ)观察图,从y=at+b,y=at2+bt+c,y=Acos(ωx+p)中选择一个合适的函数模型,并求出该拟合模型的解析式;
(Ⅲ)依据规定,当海浪高度高于1.25米时蔡对冲浪爱好者开放,请依据(Ⅱ)的结论判断一天内的8:00到20:00之间有多长时间可供冲浪爱好者进行活动.
0 239953 239961 239967 239971 239977 239979 239983 239989 239991 239997 240003 240007 240009 240013 240019 240021 240027 240031 240033 240037 240039 240043 240045 240047 240048 240049 240051 240052 240053 240055 240057 240061 240063 240067 240069 240073 240079 240081 240087 240091 240093 240097 240103 240109 240111 240117 240121 240123 240129 240133 240139 240147 266669

| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 |
(Ⅱ)观察图,从y=at+b,y=at2+bt+c,y=Acos(ωx+p)中选择一个合适的函数模型,并求出该拟合模型的解析式;
(Ⅲ)依据规定,当海浪高度高于1.25米时蔡对冲浪爱好者开放,请依据(Ⅱ)的结论判断一天内的8:00到20:00之间有多长时间可供冲浪爱好者进行活动.
 如图所示的三角形数阵叫“牛顿调和三角形”,它们是整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$,$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$,…,则第6行第3个数(从左往右数)为$\frac{1}{60}$.
如图所示的三角形数阵叫“牛顿调和三角形”,它们是整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$,$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$,…,则第6行第3个数(从左往右数)为$\frac{1}{60}$.