题目内容
9.已知定认在R上的可导函数f(x)的导函数f′(x),若对于任意实数x,有f′(x)<f(x),且y=f(x)-1为奇函数,则不等式f(x)<ex的解集为( )| A. | (0,+∞) | B. | (-∞,0) | C. | (-∞,e4) | D. | (e4,+∞) |
分析 根据条件构造函数令g(x)=$\frac{f(x)}{{e}^{x}}$,由求导公式和法则求出g′(x),根据条件判断出g′(x)的符号,得到函数g(x)的单调性,再由奇函数f(x)的结论:f(0)=0求出g(0)的值,将不等式进行转化后,利用g(x)的单调性可求出不等式的解集.
解答 解:由题意令g(x)=$\frac{f(x)}{{e}^{x}}$,
则g′(x)=$\frac{f′(x){e}^{x}-f(x)({e}^{x})′}{{e}^{2x}}$=$\frac{f′(x)-f(x)}{{e}^{x}}$,
∵f(x)>f′(x),
∴g′(x)<0,
即g(x)在R上是单调递减函数,
∵y=f(x)-1为奇函数,
∴f(0)-1=0,即f(0)=1,g(0)=1,
则不等式f(x)<ex等价为$\frac{f(x)}{{e}^{x}}$<1=g(0),
即g(x)<g(0),
解得x>0,
∴不等式的解集为(0,+∞),
故选A.
点评 本题主要考查导数与函数的单调性关系,奇函数的结论的灵活应用,以及利用条件构造函数,利用函数的单调性解不等式是解决本题的关键,考查学生的解题构造能力和转化思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.已知某海滨浴场的海浪高度(单位:米)是时间(单位:小时,0≤t≤24)的函数,记作y=f(t),如表是某日各时的浪高数据:
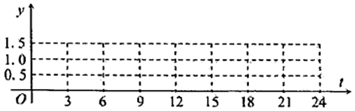
(Ⅰ)在如图的网格中描出所给的点;
(Ⅱ)观察图,从y=at+b,y=at2+bt+c,y=Acos(ωx+p)中选择一个合适的函数模型,并求出该拟合模型的解析式;
(Ⅲ)依据规定,当海浪高度高于1.25米时蔡对冲浪爱好者开放,请依据(Ⅱ)的结论判断一天内的8:00到20:00之间有多长时间可供冲浪爱好者进行活动.

| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 |
(Ⅱ)观察图,从y=at+b,y=at2+bt+c,y=Acos(ωx+p)中选择一个合适的函数模型,并求出该拟合模型的解析式;
(Ⅲ)依据规定,当海浪高度高于1.25米时蔡对冲浪爱好者开放,请依据(Ⅱ)的结论判断一天内的8:00到20:00之间有多长时间可供冲浪爱好者进行活动.
1.在△ABC中,内角A,B,C所对应的边分别为a,b,c,且a=3b,4bsinC=c,则sinA等于( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{9}$ | D. | $\frac{3}{16}$ |
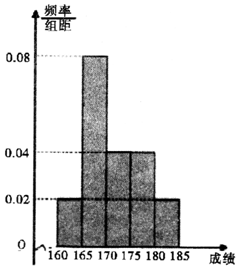 近期中央电视台播出的《中国诗词大会》火遍全国.某选拔赛后,随机抽取100名选手的成绩,按成绩由低到高依次分为第1,2,3,4,5组,制成频率分布直方图如图所示:
近期中央电视台播出的《中国诗词大会》火遍全国.某选拔赛后,随机抽取100名选手的成绩,按成绩由低到高依次分为第1,2,3,4,5组,制成频率分布直方图如图所示: