题目内容
8.4个不同的小球全部随意放入3个不同的盒子里,使每个盒子都不空的放法种数为( )| A. | C${\;}_{4}^{1}$C${\;}_{4}^{3}$C${\;}_{2}^{2}$ | B. | A${\;}_{3}^{1}$A${\;}_{4}^{3}$ | ||
| C. | C${\;}_{4}^{3}$A${\;}_{2}^{2}$ | D. | ${C}_{4}^{2}{A}_{3}^{3}$ |
分析 正确把4个不同的小球分成三份,再把这不同的三份全排列,利用乘法原理即可.
解答 解:把4个不同的小球分成三份有${C}_{4}^{2}$,这些不同的分法,每一份全排列有${A}_{3}^{3}$种方法.
根据乘法原理可得:4个不同的小球全部随意放入3个不同的盒子里,使每个盒子都不空的放法种数为${C}_{4}^{2}{A}_{3}^{3}$.
故选:D.
点评 正确理解排列、组合及乘法原理的意义是解题的关键.

练习册系列答案
相关题目
19.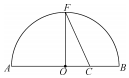 《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点F在半圆O上,点C在直径AB上,且OF⊥AB,设AC=a,BC=b,则该图形可以完成的无字证明为( )
《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点F在半圆O上,点C在直径AB上,且OF⊥AB,设AC=a,BC=b,则该图形可以完成的无字证明为( )
 《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点F在半圆O上,点C在直径AB上,且OF⊥AB,设AC=a,BC=b,则该图形可以完成的无字证明为( )
《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点F在半圆O上,点C在直径AB上,且OF⊥AB,设AC=a,BC=b,则该图形可以完成的无字证明为( )| A. | $\frac{a+b}{2}≥\sqrt{ab}$(a>0,b>0) | B. | a2+b2≥2ab(a>0,b>0) | ||
| C. | $\frac{2ab}{a+b}≤\sqrt{ab}$(a>0,b>0) | D. | $\frac{a+b}{2}≤\sqrt{\frac{{{a^2}+{b^2}}}{2}}$(a>0,b>0) |
16. 将一张边长为12cm的正方形纸片按如图(1)所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型,如图(2)所示放置.如果正四棱锥的主视图是等边三角形,如图(3)所示,则正四棱锥的体积是( )
将一张边长为12cm的正方形纸片按如图(1)所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型,如图(2)所示放置.如果正四棱锥的主视图是等边三角形,如图(3)所示,则正四棱锥的体积是( )
 将一张边长为12cm的正方形纸片按如图(1)所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型,如图(2)所示放置.如果正四棱锥的主视图是等边三角形,如图(3)所示,则正四棱锥的体积是( )
将一张边长为12cm的正方形纸片按如图(1)所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型,如图(2)所示放置.如果正四棱锥的主视图是等边三角形,如图(3)所示,则正四棱锥的体积是( )| A. | $\frac{32}{3}$$\sqrt{6}$cm3 | B. | $\frac{64}{3}$$\sqrt{6}$cm3 | C. | $\frac{32}{3}$$\sqrt{2}$cm3 | D. | $\frac{64}{3}$$\sqrt{2}$cm3 |
3.“孝敬父母,感恩社会”是中华民族的传统美德,从出生开始,父母就对我们关心无微不至,其中对我们物质帮助是最重要的一个指标,下表是一个统计员在统计《父母为我花了多少》当中使用处理得到下列的数据:
参考数据公式:$\sum_{i=1}^{6}$xiyi=1024.6,$\sum_{i=1}^{6}$xi2=730,$\overline{x}$=9,$\overline{y}$=$\frac{379}{30}$
线性回归方程:$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$
假设花费累积y与岁数x符合线性相关关系,求:
(1)花费累积y与岁数x的线性回归直线方程(系数保留3位小数);
(2)24岁大学毕业之后,我们不再花父母的钱,假设你在30岁成家立业之后,在你50岁之前偿还父母为你的花费(不计利总),那么你每月要偿还父母约多少元钱?
参考数据公式:$\sum_{i=1}^{6}$xiyi=1024.6,$\sum_{i=1}^{6}$xi2=730,$\overline{x}$=9,$\overline{y}$=$\frac{379}{30}$
线性回归方程:$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$
| 岁数x | 1 | 2 | 6 | 12 | 16 | 17 |
| 花费累积y(万元) | 1 | 2.8 | 9 | 17 | 22 | 24 |
(1)花费累积y与岁数x的线性回归直线方程(系数保留3位小数);
(2)24岁大学毕业之后,我们不再花父母的钱,假设你在30岁成家立业之后,在你50岁之前偿还父母为你的花费(不计利总),那么你每月要偿还父母约多少元钱?
13.如图所示给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图,其中判断框内应填入的条件是( )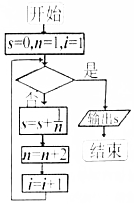

| A. | i>1010 | B. | i<1010 | C. | i>1009 | D. | i<1009 |
20.在△ABC中,已知a=5,b=5$\sqrt{3}$.C=30°,则角C的对边c的长为( )
| A. | 5$\sqrt{13}$ | B. | 5$\sqrt{11}$ | C. | 5$\sqrt{7}$ | D. | 5 |
17.“直线y=x+b与圆x2+y2=1相交”是“0<b<1”的( )条件.
| A. | 充要 | B. | 充分不必要 | ||
| C. | 必要不充分 | D. | 既不充分也不必要 |
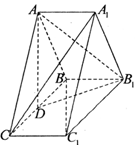 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,D为棱BC的中点,AB=AC,BC=$\sqrt{2}A{A_1}$,求证:
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,D为棱BC的中点,AB=AC,BC=$\sqrt{2}A{A_1}$,求证: