题目内容
7.下面几种推理中是演绎推理的为( )| A. | 科学家利用鱼的沉浮原理制造潜艇 | |
| B. | 猜想数列$\frac{1}{1×2}$,$\frac{1}{2×3}$,$\frac{1}{3×4}$,…的通项公式为an=$\frac{1}{n(n+1)}$(n∈N+) | |
| C. | 半径为r的圆的面积S=πr2,则单位圆的面积S=π | |
| D. | 由平面直角坐标系中圆的方程为(x-a)2+(y-b)2=r2,推测空间直角坐标系中球的方程为(x-a)2+(y-b)2+(z-c)2=r2 |
分析 本题考查的是演绎推理的定义,判断一个推理过程是否是演绎推理关键是看他是否符合演绎推理的定义,能否从推理过程中找出“三段论”的三个组成部分.
解答 解:选项B是由特殊到一般的推理过程,为归纳推理;
选项C:半径为r圆的面积S=πr2,因为单位圆的半径为1,则单位圆的面积S=π中,
半径为r圆的面积S=πr2,是大前提
单位圆的半径为1,是小前提
单位圆的面积S=π为结论;
选项A,D是由特殊到与它类似的另一个特殊的推理过程,是类比推理,
故选:C.
点评 判断一个推理过程是否是归纳推理关键是看它是否符合归纳推理的定义,即是否是由特殊到一般的推理过程.判断一个推理过程是否是类比推理关键是看它是否符合类比推理的定义,即是否是由特殊到与它类似的另一个特殊的推理过程.判断一个推理过程是否是演绎推理关键是看它是否符合演绎推理的定义,能否从推理过程中找出“三段论”的三个组成部分.

练习册系列答案
相关题目
12.复平面上平行四边形ABCD的四个顶点中,A、B、C所对应的复数分别为2-3i、-2-3i、-3+2i,则D点对应的复数是( )
| A. | 1+2i | B. | 1-2i | C. | 2-i | D. | 2+i |
19.为了对2016年某校中考成绩进行分析,在60分以上的全体同学中随机抽取8位,他们的数学、物理、化学分数(折算成百分制)事实上对应如表:
(1)若规定80分以上为优秀,请填写如下2×2列联表,问是否有90%的把握认为是否优秀与科目有关;
(2)用变量y与x,z与x的相关系数说明物理与数学、化学与数学的相关程度;
(3)求y与x,z与x的线性回归方程(系数精确到0,01),当某位同学的数学成绩为50分时,估计其物理、化学两科的成绩.
参考公式:相关系数r=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}•\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}$,
回归直线方程是:$\widehat{y}$=bx+a,其中b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,a=$\overline{y}$-b$\overline{x}$,
参考数据:$\overline{x}$=77.5,$\overline{y}$=85,$\overline{z}$=81,$\sum_{i=1}^{8}$(xi-$\overline{x}$)2≈1050,$\sum_{i=1}^{8}$(yi-$\overline{y}$)2≈456,$\sum_{i=1}^{8}$(zi-$\overline{z}$)2≈550,≈688,$\sum_{i=1}^{8}$(xi-$\overline{x}$)(zi-$\overline{z}$)≈755,$\sqrt{1050}$≈32.4,$\sqrt{456}$≈21.4,$\sqrt{550}$≈23.5.
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
| 化学分数z | 67 | 72 | 76 | 80 | 84 | 87 | 90 | 92 |
| 优秀 | 不优秀 | 合计 | |
| 数学 | |||
| 物理 | |||
| 合计 |
(3)求y与x,z与x的线性回归方程(系数精确到0,01),当某位同学的数学成绩为50分时,估计其物理、化学两科的成绩.
参考公式:相关系数r=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}•\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}$,
回归直线方程是:$\widehat{y}$=bx+a,其中b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,a=$\overline{y}$-b$\overline{x}$,
参考数据:$\overline{x}$=77.5,$\overline{y}$=85,$\overline{z}$=81,$\sum_{i=1}^{8}$(xi-$\overline{x}$)2≈1050,$\sum_{i=1}^{8}$(yi-$\overline{y}$)2≈456,$\sum_{i=1}^{8}$(zi-$\overline{z}$)2≈550,≈688,$\sum_{i=1}^{8}$(xi-$\overline{x}$)(zi-$\overline{z}$)≈755,$\sqrt{1050}$≈32.4,$\sqrt{456}$≈21.4,$\sqrt{550}$≈23.5.
 如图,已知正四棱柱(底面为正方形,侧棱与底面垂直)ABCD-A1B1C1D1的底面边长为3,侧棱长为4,连结A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.
如图,已知正四棱柱(底面为正方形,侧棱与底面垂直)ABCD-A1B1C1D1的底面边长为3,侧棱长为4,连结A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.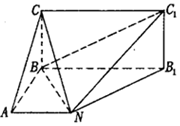 如图,已知矩形BB1C1C所在平面与底面ABB1N垂直,在直角梯形ABB1N中,AN∥BB1,AB⊥AN,CB=BA=AN=$\frac{1}{2}$BB1.
如图,已知矩形BB1C1C所在平面与底面ABB1N垂直,在直角梯形ABB1N中,AN∥BB1,AB⊥AN,CB=BA=AN=$\frac{1}{2}$BB1.