19.已知f(x)是定义在R上的奇函数,且f(x+2)=f(x-2);当0≤x≤1时,f(x)=$\sqrt{x}$,则f(1)+f(2)+f(3)+…+f(2017)等于( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
18.某四棱台的三视图如图所示,则该四棱台的体积是( )
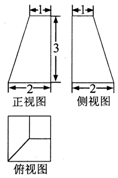

| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
17.在平面直角坐标系xOy中,以坐标原点为圆心且与直线mx-y-2m+1=0(m∈R)相切的所有圆中,半径最大的圆的标准方程为( )
| A. | x2+y2=5 | B. | x2+y2=3 | C. | x2+y2=9 | D. | x2+y2=7 |
16.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}$=(1,-1),|$\overrightarrow{b}$|=1,且$\overrightarrow{b}$⊥($\overrightarrow{a}$+$\overrightarrow{b}$),则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{3π}{4}$ |
15.已知函数f(x)=sinωx+$\sqrt{3}$cosωx(x∈R),又f(α)=2,f(β)=2,且|α-β|的最小值是$\frac{π}{2}$,则正数ω的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
13.已知集合A={x|y=log2(x-1)},集合B={x|(x+1)(x-2)≤0},则A∪B=( )
| A. | [-1,+∞) | B. | (1,2] | C. | (1,+∞) | D. | [-1,2] |
11.某公司有A、B、C、D、E五辆汽车,其中A、B两辆汽车的车牌尾号均为1,C、D两辆汽车的车牌尾号均为2,E车的车牌尾号为6.已知在非限行日,每辆车可能出车或不出车,A、B、E三辆汽车每天出车的概率均为$\frac{2}{3}$,C、D两辆汽车每天出车的概率均为$\frac{1}{2}$,五辆汽车是否出车相互独立,该公司所在地区汽车限行规定如下:
例如,星期一禁止车牌尾号为0和5的车辆通行.
(1)求该公司在星期一至少有2辆汽车出车的概率;
(2)设X表示该公司在星期二和星期三两天出车的车辆数之和,求X的分布列及数学期望.
0 239945 239953 239959 239963 239969 239971 239975 239981 239983 239989 239995 239999 240001 240005 240011 240013 240019 240023 240025 240029 240031 240035 240037 240039 240040 240041 240043 240044 240045 240047 240049 240053 240055 240059 240061 240065 240071 240073 240079 240083 240085 240089 240095 240101 240103 240109 240113 240115 240121 240125 240131 240139 266669
| 工作日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
| 限行车牌尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
(1)求该公司在星期一至少有2辆汽车出车的概率;
(2)设X表示该公司在星期二和星期三两天出车的车辆数之和,求X的分布列及数学期望.
 如图,四棱锥P-ABCD的底面是等腰梯形,AD∥BC,BC=2AD,O为BD的中点.
如图,四棱锥P-ABCD的底面是等腰梯形,AD∥BC,BC=2AD,O为BD的中点.