题目内容
13.已知集合A={x|y=log2(x-1)},集合B={x|(x+1)(x-2)≤0},则A∪B=( )| A. | [-1,+∞) | B. | (1,2] | C. | (1,+∞) | D. | [-1,2] |
分析 求函数y=log2(x-1)的定义域可得集合A,解不等式可得集合B,由集合并集的定义即可得答案.
解答 解:根据题意,对于函数y=log2(x-1),有x-1>0,解可得x>1,
即函数y=log2(x-1)的定义域为(1,+∞),
A为函数y=log2(x-1)的定义域,则A=(1,+∞),
集合B={x|(x+1)(x-2)≤0}={x|-1≤x≤2}=[-1,2],
则A∪B=[-1,+∞);
故选:A.
点评 本题考查集合并集的计算,注意集合A、B的意义,

练习册系列答案
相关题目
1.若复数$\frac{a+i}{1+2i}({a∈R})$为纯虚数,其中i为虚数单位,则a=( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | $-\frac{1}{2}$ |
18.某四棱台的三视图如图所示,则该四棱台的体积是( )
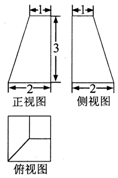

| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
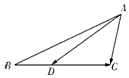 如图,在△ABC中,∠BAC=60°,AB=2,AC=1,D是BC边上一点,且$\overrightarrow{CD}$=2$\overrightarrow{DB}$,则$\overrightarrow{AD}$•$\overrightarrow{BC}$ 的值为-2.
如图,在△ABC中,∠BAC=60°,AB=2,AC=1,D是BC边上一点,且$\overrightarrow{CD}$=2$\overrightarrow{DB}$,则$\overrightarrow{AD}$•$\overrightarrow{BC}$ 的值为-2.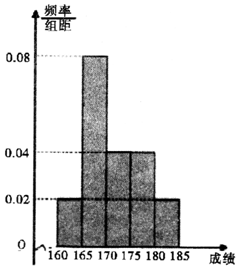 近期中央电视台播出的《中国诗词大会》火遍全国.某选拔赛后,随机抽取100名选手的成绩,按成绩由低到高依次分为第1,2,3,4,5组,制成频率分布直方图如图所示:
近期中央电视台播出的《中国诗词大会》火遍全国.某选拔赛后,随机抽取100名选手的成绩,按成绩由低到高依次分为第1,2,3,4,5组,制成频率分布直方图如图所示: