题目内容
18．某四棱台的三视图如图所示，则该四棱台的体积是（ ）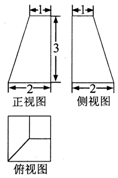
| A． | 7 | B． | 6 | C． | 5 | D． | 4 |
分析 根据四棱台的三视图，得出该四棱台的结构特征是什么，由此计算它的体积即可．
解答 
解：由几何体的三视图得到几何体是上下底面都是正方形的棱台如图：
根据图中数据得到棱台的体积为$\frac{1}{3}×（{2}^{2}+{1}^{2}+\sqrt{{1}^{2}×{2}^{2}}）×3$=7；
故选A．
点评 本题考查三视图与几何体的关系，棱台体积公式的应用，考查计算能力与空间想象能力．
练习册系列答案
相关题目
8．设函数f（x）=$\left\{\begin{array}{l}{-|lnx|，x＞0}\\{{x}^{2}+2x-1，x≤0}\end{array}\right.$，若f（a）=f（b）=f（c）=f（d），其中a，b，c，d互不相等，则对于命题p：abcd∈（0，1）和命题q：a+b+c+d∈[e+e-1-2，e2+e-2-2）真假的判断，正确的是（ ）
| A． | p假q真 | B． | p假q假 | C． | p真q真 | D． | p真q假 |
13．已知集合A={x|y=log2（x-1）}，集合B={x|（x+1）（x-2）≤0}，则A∪B=（ ）
| A． | [-1，+∞） | B． | （1，2] | C． | （1，+∞） | D． | [-1，2] |
4．如图，某港口一天的水深变化曲线近似满足函数y=Asin$\frac{π}{6}$t+k，则水深从最小值变化到最大值至少需要（ ）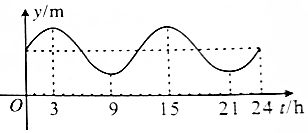
| A． | 6h | B． | 8h | C． | 12h | D． | 24h |
1．为了普及环保知识，增强环保意识，某大学从大学理工类专业的A班和文史专业的B班各抽取20名同学参加环保知识测试，统计得到成绩与专业的列联表：
附：参考公式及数据：
①K2统计量：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$（其中n=a+b+c+d）；
②独立性检验的临界值表：
（ ）
| 优秀 | 非优秀 | 总计 | |
| A班 | 14 | 6 | 20 |
| B班 | 7 | 13 | 20 |
| 总计 | 21 | 19 | 40 |
①K2统计量：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$（其中n=a+b+c+d）；
②独立性检验的临界值表：
| P（K≥k0） | 0.050 | 0.010 |
| k0 | 3.841 | 6.635 |
| A． | 有99%的把握认为环保知识测试成绩与专业有关 | |
| B． | 有99%的把握认为环保知识测试成绩与专业无关 | |
| C． | 有95%的把握认为环保知识测试成绩与专业无关 | |
| D． | 有95%的把握认为环保知识测试成绩与专业有关 |