14.设z=$\frac{10i}{3+i}$,则$\overline{z}$=( )
| A. | -1+3i | B. | -1-3i | C. | 1+3i | D. | 1-3i |
10.曲线y=lgx在x=1处的切线斜率是( )
| A. | $\frac{1}{ln10}$ | B. | ln10 | C. | lne | D. | $\frac{1}{lne}$ |
9.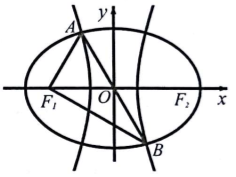 如图,F1、F2是椭圆C1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若AF1⊥BF1,且∠AF1O=$\frac{π}{3}$,则C1与C2的离心率之和为( )
如图,F1、F2是椭圆C1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若AF1⊥BF1,且∠AF1O=$\frac{π}{3}$,则C1与C2的离心率之和为( )
 如图,F1、F2是椭圆C1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若AF1⊥BF1,且∠AF1O=$\frac{π}{3}$,则C1与C2的离心率之和为( )
如图,F1、F2是椭圆C1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若AF1⊥BF1,且∠AF1O=$\frac{π}{3}$,则C1与C2的离心率之和为( )| A. | 2$\sqrt{3}$ | B. | 4 | C. | 2$\sqrt{5}$ | D. | 2$\sqrt{6}$ |
8.三棱锥D-ABC中,AB=CD=$\sqrt{6}$,其余四条棱长均为2,则三棱锥D-ABC的外接球的表面积为( )
| A. | 14π | B. | 7π | C. | 21π | D. | 28π |
7.已知函数f(x)=$\frac{\sqrt{3}}{2}$sinωx-$\frac{1}{2}$cosωx(ω>0),将函数y=|f(x)|的图象向左平移$\frac{π}{9}$个单位长度后关于y轴对称,则当ω取最小值时,g(x)=cos(ωx+$\frac{π}{4}$)的单调递减区间为( )
| A. | [-$\frac{π}{3}$+$\frac{2kπ}{3}$,$\frac{π}{2}$+$\frac{2kπ}{3}$](k∈Z) | B. | [-$\frac{π}{3}$+$\frac{4kπ}{3}$,$\frac{π}{2}$+$\frac{4kπ}{3}$](k∈Z) | ||
| C. | [-$\frac{π}{6}$+$\frac{2kπ}{3}$,$\frac{π}{2}$+$\frac{2kπ}{3}$](k∈Z) | D. | [-$\frac{π}{6}$+$\frac{4kπ}{3}$,$\frac{π}{2}$+$\frac{4kπ}{3}$](k∈Z) |
6.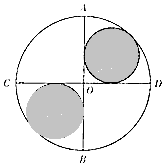 如图所示,已知AB,CD是圆O中两条互相垂直的直径,两个小圆与圆O以及AB,CD均相切,则往圆O内投掷一个点,该点落在阴影部分的概率为( )
如图所示,已知AB,CD是圆O中两条互相垂直的直径,两个小圆与圆O以及AB,CD均相切,则往圆O内投掷一个点,该点落在阴影部分的概率为( )
0 239913 239921 239927 239931 239937 239939 239943 239949 239951 239957 239963 239967 239969 239973 239979 239981 239987 239991 239993 239997 239999 240003 240005 240007 240008 240009 240011 240012 240013 240015 240017 240021 240023 240027 240029 240033 240039 240041 240047 240051 240053 240057 240063 240069 240071 240077 240081 240083 240089 240093 240099 240107 266669
 如图所示,已知AB,CD是圆O中两条互相垂直的直径,两个小圆与圆O以及AB,CD均相切,则往圆O内投掷一个点,该点落在阴影部分的概率为( )
如图所示,已知AB,CD是圆O中两条互相垂直的直径,两个小圆与圆O以及AB,CD均相切,则往圆O内投掷一个点,该点落在阴影部分的概率为( )| A. | 12-8$\sqrt{2}$ | B. | 3-2$\sqrt{2}$ | C. | 8-5$\sqrt{2}$ | D. | 6-4$\sqrt{2}$ |