题目内容
6.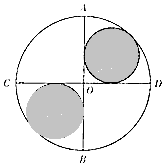 如图所示,已知AB,CD是圆O中两条互相垂直的直径,两个小圆与圆O以及AB,CD均相切,则往圆O内投掷一个点,该点落在阴影部分的概率为( )
如图所示,已知AB,CD是圆O中两条互相垂直的直径,两个小圆与圆O以及AB,CD均相切,则往圆O内投掷一个点,该点落在阴影部分的概率为( )| A. | 12-8$\sqrt{2}$ | B. | 3-2$\sqrt{2}$ | C. | 8-5$\sqrt{2}$ | D. | 6-4$\sqrt{2}$ |
分析 由题意,本题是几何概型,只要利用阴影部分的面积与圆O的面积比求概率.
解答 解:设小圆半径为r,则圆O的半径为r+$\sqrt{2}$r,由几何概型的公式得到:往圆O内投掷一个点,该点落在阴影部分的概率为:r+$\frac{2π{r}^{2}}{π(1+\sqrt{2})^{2}{r}^{2}}=6-4\sqrt{2}$;
故选:D.
点评 本题考查了几何概型的概率求法;关键是明确几何测度为面积,利用面积比求概率.

练习册系列答案
相关题目
16.下列函数中,与函数y=x3的单调性和奇偶性一致的函数是( )
| A. | $y=\sqrt{x}$ | B. | y=tanx | C. | $y=x+\frac{1}{x}$ | D. | y=ex-e-x |
17.$({x+\frac{1}{x}}){({2x-\frac{1}{x}})^5}$是展开式的常数项为( )
| A. | 120 | B. | 40 | C. | -40 | D. | 80 |
1.函数$y=\sqrt{x}+\sqrt{1-x}$的最大值为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |