题目内容
11.点(3,4)不在不等式y≤3x+b表示的区域内,而点(4,4)在此区域内,则实数b的取值范围是[-8,-5).分析 根据二元一次不等式表示平面区域,结合点和不等式的关系进行转化求解即可.
解答 解:∵点(3,4)不在不等式y≤3x+b表示的区域内,而点(4,4)在此区域内,
∴$\left\{\begin{array}{l}{4>3×3+b}\\{4≤4×3+b}\end{array}\right.$,即$\left\{\begin{array}{l}{b<-5}\\{b≥-8}\end{array}\right.$,
得-8≤b<-5,即实数b的取值范围是[-8,-5),
故答案为:[-8,-5)
点评 本题主要考查不等式的求解,结合点与平面区域的关系转化为不等式关系是解决本题的关键.

练习册系列答案
相关题目
1.已知球O是正三棱锥(底面为正三角形,顶点在底面的射影为底面中心)A-BCD的外接球,BC=3,$AB=2\sqrt{3}$,点E在线段BD上,且BD=3BE,过点E作圆O的截面,则所得截面圆面积的取值范围是( )
| A. | [π,4π] | B. | [2π,4π] | C. | [3π,4π] | D. | (0,4π] |
19.已知实数a,b,c满足a2+b=lna,则(a-c)2+(b+c-2)2的最小值为( )
| A. | 2$\sqrt{2}$ | B. | 8 | C. | $\sqrt{2}$ | D. | 2 |
6.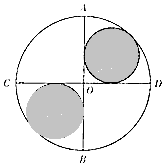 如图所示,已知AB,CD是圆O中两条互相垂直的直径,两个小圆与圆O以及AB,CD均相切,则往圆O内投掷一个点,该点落在阴影部分的概率为( )
如图所示,已知AB,CD是圆O中两条互相垂直的直径,两个小圆与圆O以及AB,CD均相切,则往圆O内投掷一个点,该点落在阴影部分的概率为( )
 如图所示,已知AB,CD是圆O中两条互相垂直的直径,两个小圆与圆O以及AB,CD均相切,则往圆O内投掷一个点,该点落在阴影部分的概率为( )
如图所示,已知AB,CD是圆O中两条互相垂直的直径,两个小圆与圆O以及AB,CD均相切,则往圆O内投掷一个点,该点落在阴影部分的概率为( )| A. | 12-8$\sqrt{2}$ | B. | 3-2$\sqrt{2}$ | C. | 8-5$\sqrt{2}$ | D. | 6-4$\sqrt{2}$ |
20.已知函数f(x)=lnx-3x,则曲线y=f(x)在点(1,f(1))处的切线与坐标轴围成的三角形的面积为( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
5.设$\frac{1}{2}$<($\frac{1}{2}$)b<($\frac{1}{2}$)a,则下列不等关系成立的是( )
| A. | aa<ab<ba | B. | aa<ba<ab | C. | ab<aa<ba | D. | ab<ba<aa |
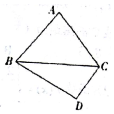 如图,在△ABC中,角A,B,C的对边分别为a,b,c,a=b(sinC+cosC).
如图,在△ABC中,角A,B,C的对边分别为a,b,c,a=b(sinC+cosC).