4.近代统计学的发展起源于二十世纪初,它是在概率论的基础上发展起来的,统计性质的工作可以追溯到远古的“结绳记事”和《二十四史》中大量的关于我人口、钱粮、水文、天文、地震等资料的记录.近几年,雾霾来袭,对某市该年11月份的天气情况进行统计,结果如下:表一
由于此种情况某市政府为减少雾霾于次年采取了全年限行的政策.
下表是一个调査机构对比以上两年11月份(该年不限行30天、次年限行30天共60天)的调查结果:
表二
(1)请由表一数据求a,b,并求在该年11月份任取一天,估计该市是晴天的概率;
(2)请用统计学原理计算若没有90%的把握认为雾霾与限行有关系,则限行时有多少天没有雾霾?
(由于不能使用计算器,所以表中数据使用时四舍五入取整数)
${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({a+d})({a+c})({b+d})}}$.
| 日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 天气 | 晴 | 霾 | 霾 | 阴 | 霾 | 霾 | 阴 | 霾 | 霾 | 霾 | 阴 | 晴 | 霾 | 霾 | 霾 |
| 日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 天气 | 霾 | 霾 | 霾 | 阴 | 晴 | 霾 | 霾 | 晴 | 霾 | 晴 | 霾 | 霾 | 霾 | 晴 | 霾 |
下表是一个调査机构对比以上两年11月份(该年不限行30天、次年限行30天共60天)的调查结果:
表二
| 不限行 | 限行 | 总计 | |
| 没有雾霾 | a | ||
| 有雾霾 | b | ||
| 总计 | 30 | 30 | 60 |
(2)请用统计学原理计算若没有90%的把握认为雾霾与限行有关系,则限行时有多少天没有雾霾?
(由于不能使用计算器,所以表中数据使用时四舍五入取整数)
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
18.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的渐近线方程为y=±$\frac{{\sqrt{3}}}{3}$x,左、右焦点分别为F1、F2,M为双曲线C的一条渐近线上某一点,且∠OMF2=$\frac{π}{2},{S_{△OM{F_2}}}=8\sqrt{3}$,则双曲线C的焦距为( )
| A. | $8\sqrt{3}$ | B. | 16 | C. | 8 | D. | $4\sqrt{3}$ |
17.$({x+\frac{1}{x}}){({2x-\frac{1}{x}})^5}$是展开式的常数项为( )
| A. | 120 | B. | 40 | C. | -40 | D. | 80 |
16.在一次实验中,同时抛掷4枚均匀的硬币16次,设4枚硬币正好出现3枚正面向上,1枚反面向上的次数为ξ,则ξ的方差是( )
0 239910 239918 239924 239928 239934 239936 239940 239946 239948 239954 239960 239964 239966 239970 239976 239978 239984 239988 239990 239994 239996 240000 240002 240004 240005 240006 240008 240009 240010 240012 240014 240018 240020 240024 240026 240030 240036 240038 240044 240048 240050 240054 240060 240066 240068 240074 240078 240080 240086 240090 240096 240104 266669
| A. | 3 | B. | 4 | C. | 1 | D. | $\frac{15}{16}$ |
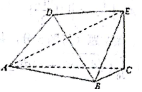 如图,以A、B、C、D、E为顶点的六面体中,△ABC和△ABD均为等边三角形,且平面ABC⊥平面ABD,EC⊥平面ABC,EC=$\sqrt{3}$,AB=2.
如图,以A、B、C、D、E为顶点的六面体中,△ABC和△ABD均为等边三角形,且平面ABC⊥平面ABD,EC⊥平面ABC,EC=$\sqrt{3}$,AB=2.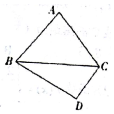 如图,在△ABC中,角A,B,C的对边分别为a,b,c,a=b(sinC+cosC).
如图,在△ABC中,角A,B,C的对边分别为a,b,c,a=b(sinC+cosC).