题目内容
5.已知函数p(x)=lnx-x+4,q(x)=$\frac{{a{e^x}}}{x}({a∈R})$.(1)若函数y=p(x),y=q(x)的图象有平行于坐标轴的公切线,求a的值;
(2)若关于x的不等式p(x)-4<q(x)的解集中有且只有两个整数,求a的取值范围.
分析 (1)求出函数的导数,求出切线斜率,得到关于a的方程,解出即可;
(2)分离参数a,令$h(x)=\frac{{xlnx-{x^2}}}{e^x}$,求出函数的导数,求出函数的最小值,从而求出a的范围即可.
解答 解:(1)由题知p'(x)=q'(x),即$\frac{1-x}{x}=\frac{{a{e^x}({x-1})}}{x^2}$,
当x=1£?p'(1)=q'(1)=0,即x=1是y=p(x),y=q(x)的极值点,
所以公切线的斜率为0,所以p(1)=q(1),lnl-1+4=ae,可得$a=\frac{3}{e}$.
(2)p(x)-4>q(x)等价于$lnx-x<\frac{{a{e^x}}}{x},a>\frac{{xlnx-{x^2}}}{e^x}$,
令$h(x)=\frac{{xlnx-{x^2}}}{e^x}$,则$h'(x)=\frac{{({x-1})({x-1-lnx})}}{e^x}$,
令φ(x)=x-lnx-1,则$φ'(x)=1-\frac{1}{x}=\frac{x-1}{x}$,
即φ(x)在(0,1)上单调递减,(1,+∞)单调递增.
φ(x)min=φ(1)=0,∴φ(x)≥0恒成立,
所以h(x)在(0,1)上单调递减,(1,+∞)单调递增.
$h{(x)_{min}}=h(1)=\frac{-1}{e},h(1)<h(2)=\frac{2ln2-4}{e^2}<h(3)=\frac{3ln3-9}{e^3}$,
因为解集中有且只有两个整数$\frac{2ln2-4}{e^2}<a≤\frac{3ln3-9}{e^3}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道综合题.

练习册系列答案
相关题目
13.已知全集U=R,集合M=$\left\{{x|{{({\frac{1}{3}})}^x}≤1}\right\},N=\left\{{x|-1<x<4}\right\}$,则M∩N=( )
| A. | {x|-1<x≤0} | B. | {x|0≤x<4} | C. | {1,2,3} | D. | {0,1,2,3} |
17.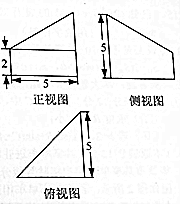 《九章算术》是中国古代第一部数学专著,书中有关于“堑堵”的记载,“堑堵”即底面是直角三角形的直三棱柱,已知某“堑堵”被一个平面截去一部分后,剩下部分的三视图如图所示,则剩下部分的体积是( )
《九章算术》是中国古代第一部数学专著,书中有关于“堑堵”的记载,“堑堵”即底面是直角三角形的直三棱柱,已知某“堑堵”被一个平面截去一部分后,剩下部分的三视图如图所示,则剩下部分的体积是( )
 《九章算术》是中国古代第一部数学专著,书中有关于“堑堵”的记载,“堑堵”即底面是直角三角形的直三棱柱,已知某“堑堵”被一个平面截去一部分后,剩下部分的三视图如图所示,则剩下部分的体积是( )
《九章算术》是中国古代第一部数学专著,书中有关于“堑堵”的记载,“堑堵”即底面是直角三角形的直三棱柱,已知某“堑堵”被一个平面截去一部分后,剩下部分的三视图如图所示,则剩下部分的体积是( )| A. | 50 | B. | 75 | C. | 25.5 | D. | 37.5 |
14.设z=$\frac{10i}{3+i}$,则$\overline{z}$=( )
| A. | -1+3i | B. | -1-3i | C. | 1+3i | D. | 1-3i |
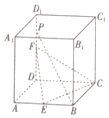 如图,在棱长为4的正方体ABCD-A1B1C1D1中,E、F分别是AB、DD1的中点,点P是DD1上一点,且PB∥平面CEF,则四棱锥P-ABCD外接球的表面积为41π.
如图,在棱长为4的正方体ABCD-A1B1C1D1中,E、F分别是AB、DD1的中点,点P是DD1上一点,且PB∥平面CEF,则四棱锥P-ABCD外接球的表面积为41π.