题目内容
19.已知变量x,y满足约束条件$\left\{\begin{array}{l}y≤x\\ x+y≥1\\ y≥3x-6\end{array}\right.$,则x2+y2+2(x-y)的最小值为$\frac{1}{2}$.分析 z=x2+y2+2(x-y)=(x+1)2+(y-1)2-2利用z的几何意义,利用数形结合即可得到结论.
解答 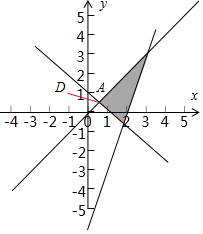 解:作出变量x,y满足约束条件$\left\{\begin{array}{l}y≤x\\ x+y≥1\\ y≥3x-6\end{array}\right.$,对应的平面区域如图
解:作出变量x,y满足约束条件$\left\{\begin{array}{l}y≤x\\ x+y≥1\\ y≥3x-6\end{array}\right.$,对应的平面区域如图
z=x2+y2+2(x-y)=(x+1)2+(y-1)2-2,则z的几何意义是,区域内的点到点D(-1,1)的距离的平方减2,
$\left\{\begin{array}{l}{y=x}\\{x+y=1}\end{array}\right.$解得A($\frac{1}{2}$,$\frac{1}{2}$)
由图象可知点D到A的距离d即为z=d2-2最小值,
则z=$\frac{1}{4}+\frac{1}{4}+2(\frac{1}{2}-\frac{1}{2})$=$\frac{1}{2}$,
故x2+y2+2(x-y)的最小值为$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题主要考查线性规划的应用,利用z的几何意义,结合点到直线的距离公式是解决本题的关键.

练习册系列答案
相关题目
14.若复数z=$\frac{{{i^{2017}}}}{1-i}$(i是虚数单位),则复数z在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
4.近代统计学的发展起源于二十世纪初,它是在概率论的基础上发展起来的,统计性质的工作可以追溯到远古的“结绳记事”和《二十四史》中大量的关于我人口、钱粮、水文、天文、地震等资料的记录.近几年,雾霾来袭,对某市该年11月份的天气情况进行统计,结果如下:表一
由于此种情况某市政府为减少雾霾于次年采取了全年限行的政策.
下表是一个调査机构对比以上两年11月份(该年不限行30天、次年限行30天共60天)的调查结果:
表二
(1)请由表一数据求a,b,并求在该年11月份任取一天,估计该市是晴天的概率;
(2)请用统计学原理计算若没有90%的把握认为雾霾与限行有关系,则限行时有多少天没有雾霾?
(由于不能使用计算器,所以表中数据使用时四舍五入取整数)
${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({a+d})({a+c})({b+d})}}$.
| 日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 天气 | 晴 | 霾 | 霾 | 阴 | 霾 | 霾 | 阴 | 霾 | 霾 | 霾 | 阴 | 晴 | 霾 | 霾 | 霾 |
| 日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 天气 | 霾 | 霾 | 霾 | 阴 | 晴 | 霾 | 霾 | 晴 | 霾 | 晴 | 霾 | 霾 | 霾 | 晴 | 霾 |
下表是一个调査机构对比以上两年11月份(该年不限行30天、次年限行30天共60天)的调查结果:
表二
| 不限行 | 限行 | 总计 | |
| 没有雾霾 | a | ||
| 有雾霾 | b | ||
| 总计 | 30 | 30 | 60 |
(2)请用统计学原理计算若没有90%的把握认为雾霾与限行有关系,则限行时有多少天没有雾霾?
(由于不能使用计算器,所以表中数据使用时四舍五入取整数)
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
11.函数f(x)=ex-4x的递减区间为( )
| A. | (0,ln4) | B. | (0,4) | C. | (-∞,ln4) | D. | (ln4,+∞) |
8.三棱锥D-ABC中,AB=CD=$\sqrt{6}$,其余四条棱长均为2,则三棱锥D-ABC的外接球的表面积为( )
| A. | 14π | B. | 7π | C. | 21π | D. | 28π |