题目内容
3.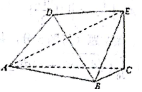 如图,以A、B、C、D、E为顶点的六面体中,△ABC和△ABD均为等边三角形,且平面ABC⊥平面ABD,EC⊥平面ABC,EC=$\sqrt{3}$,AB=2.
如图,以A、B、C、D、E为顶点的六面体中,△ABC和△ABD均为等边三角形,且平面ABC⊥平面ABD,EC⊥平面ABC,EC=$\sqrt{3}$,AB=2.(1)求证:DE⊥平面ABD;
(2)求二面角D-BE-C的余弦值.
分析 (1)作作DF⊥AB,交AB于F,连结CF.由△ABC和△ABD均为边长为2的等边三角形,得DF=$DF=\sqrt{3}$,DF=EC,于是 DE∥CF.由CF⊥平面△ABD,得DE⊥平面△ABD.
(2)由(1)知BF,CF,DF两两垂直,如图建系,则$F({0,0,0}),B({1,0,0}),D({0,0,\sqrt{3}}),C({0,\sqrt{3},0}),E({0,\sqrt{3},\sqrt{3}})$.
求出平面BDE的法向量、平面BCE的法向量,可得$cos<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{3}{4}$,即二面角D-BE-C的正弦值为$\frac{3}{4}$.
解答 解:(1)证明:作DF⊥AB,交AB于F,连结CF.因为平面ABC⊥平面ABD,
所以DF⊥平面ABC,又因为EC⊥平面ABC,从而DF∥EC,
因为,△ABC和△ABD均为边长为2的等边三角形,所以DF=$DF=\sqrt{3}$,因此DF=EC,
于是四边形DECF为平行四边形,所以DE∥CF.
因为△ABD是等边三角形,所以F是AB中点,而△ABC是等边三角形,
因此CF⊥AB,从而CF⊥平面△ABD,又因为DE∥FC,所以DE⊥平面△ABD.

(2)由(1)知BF,CF,DF两两垂直,如图建系,则$F({0,0,0}),B({1,0,0}),D({0,0,\sqrt{3}}),C({0,\sqrt{3},0}),E({0,\sqrt{3},\sqrt{3}})$.
设平面BDE的法向量$\overrightarrow m=({x,y,z})$,
由$\left\{\begin{array}{l}\overrightarrow m?¤\overrightarrow{BD}=0\\ \overrightarrow m?¤\overrightarrow{BE}=0\end{array}\right.⇒\left\{\begin{array}{l}-x+\sqrt{3}z=0\\-x+\sqrt{3}y+\sqrt{3}z=0\end{array}\right.$,令x=3得,平面BDE的法向量$\overrightarrow m=({3,0,\sqrt{3}})$;
同理可求得平面BCE的法向量$\overrightarrow n=({3,\sqrt{3},0})$,
所以$cos<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{3}{4}$,即二面角D-BE-C的余弦值为$\frac{3}{4}$.
点评 本题考查了空间线面位置关系的判定,向量法求二面角,属于中档题,

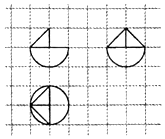
| A. | $\frac{2π+1}{3}$ | B. | $\frac{4π+1}{3}$ | C. | $\frac{2π+3}{3}$ | D. | $\frac{2π+2}{3}$ |
| A. | $8\sqrt{3}$ | B. | 16 | C. | 8 | D. | $4\sqrt{3}$ |
| A. | 3 | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
| A. | x+3y+1=0 | B. | x+3y-1=0 | C. | 3x-y-3=0 | D. | 3x+y-3=0 |
 如图所示,在三棱柱ABC-A1B1C1中,AA1B1B为正方形,BB1C1C为菱形,B1C⊥AC1.
如图所示,在三棱柱ABC-A1B1C1中,AA1B1B为正方形,BB1C1C为菱形,B1C⊥AC1.