15.△ABC的三个内角A、B、C,所对的边分别是a、b、c,若c=2$\sqrt{3}$,tanA+tanB=$\sqrt{3}$-$\sqrt{3}$tanAtanB,则△ABC的面积的取值范围是( )
| A. | [$\sqrt{3}$,+∞) | B. | (0,$\sqrt{3}$] | C. | ($\frac{1}{2}$,$\sqrt{3}$] | D. | (0,$\frac{\sqrt{3}}{2}$] |
14.已知函数f(x)为定义域在R上的奇函数,当x>0,f(x)=lnx-2x-f(1),则当x<0时,f(x)的表达式为( )
| A. | f(x)=ln(-x)+2x+1 | B. | f(x)=-ln(-x)-2x+1 | C. | f(x)=-ln(-x)-2x-1 | D. | f(x)=-ln(-x)+2x-1 |
13.设x,y满足约束条件$\left\{\begin{array}{l}{2x+y-5≤0}\\{x-y-1≤0}\\{x≥1}\end{array}\right.$,若z=ax+y仅在点(2,1)处取得最大值,则a的取值范围是( )
| A. | (-∞,-1) | B. | (2,+∞) | C. | (0,2) | D. | (-1,+∞) |
12. 已知输入的x=11,执行如图所示的程序框图,则输出的x的值为( )
已知输入的x=11,执行如图所示的程序框图,则输出的x的值为( )
 已知输入的x=11,执行如图所示的程序框图,则输出的x的值为( )
已知输入的x=11,执行如图所示的程序框图,则输出的x的值为( )| A. | 12 | B. | 23 | C. | 47 | D. | 95 |
11.抛物线y2=4x上有两点A、B到焦点的距离之和为8,则A、B到y轴的距离之和为( )
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
8.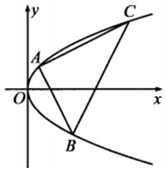 已知A、B、C是抛物线y2=2px(p>0)上三个不同的点,且AB⊥AC.
已知A、B、C是抛物线y2=2px(p>0)上三个不同的点,且AB⊥AC.
(Ⅰ)若A(1,2),B(4,-4),求点C的坐标;
(Ⅱ)若抛物线上存在点D,使得线段AD总被直线BC平分,求点A的坐标.
0 239879 239887 239893 239897 239903 239905 239909 239915 239917 239923 239929 239933 239935 239939 239945 239947 239953 239957 239959 239963 239965 239969 239971 239973 239974 239975 239977 239978 239979 239981 239983 239987 239989 239993 239995 239999 240005 240007 240013 240017 240019 240023 240029 240035 240037 240043 240047 240049 240055 240059 240065 240073 266669
 已知A、B、C是抛物线y2=2px(p>0)上三个不同的点,且AB⊥AC.
已知A、B、C是抛物线y2=2px(p>0)上三个不同的点,且AB⊥AC.(Ⅰ)若A(1,2),B(4,-4),求点C的坐标;
(Ⅱ)若抛物线上存在点D,使得线段AD总被直线BC平分,求点A的坐标.