题目内容

10．设集合A={x|x2-9＜0}，B={-3，-1，0，2，3}，则A∩B中元素的个数为（　　）
A．3B．4C．5D．6

分析 解关于A的不等式，求出A、B的交集即可．

解答 解：A={x|x2-9＜0}={x|-3＜x＜3}，
B={-3，-1，0，2，3}，
则A∩B={-1，0，2}，
共3个元素，
故选：A．

点评 本题考查了集合的运算，考查不等式问题，是一道基础题．

练习册系列答案
相关题目
20．在△ABC中，a=$\sqrt{7}$，b=2，A=60°，则c=（　　）
A．1B．2C．3D．4
1．定义max{a，b}=$\left\{\begin{array}{l}{a，a≥b}\\{b，a＜b}\end{array}\right.$，已知函数f（x）=max{|2x-1|，ax2+b}，其中a＜0，b∈R，若f（0）=b，则实数b的范围为[1，+∞），若f（x）的最小值为1，则a+b=1．
18．已知等差数列{an}满足a5=8，a7=12．
（1）求数列{an}的通项公式；
（2）设等比数列{bn}的各项均为正数，其前n项和为Tn，若b3=a3，T2=3，求Tn．
5．给定R上的函数f（x），（　　）
A．存在R上函数g（x），使得f（g（x））=xB．存在R上函数g（x），使得g（f（x））=x
C．存在R上函数g（x），使得f（g（x））=g（x）D．存在R上函数g（x），使得f（g（x））=g（f（x））
15．△ABC的三个内角A、B、C，所对的边分别是a、b、c，若c=2$\sqrt{3}$，tanA+tanB=$\sqrt{3}$-$\sqrt{3}$tanAtanB，则△ABC的面积的取值范围是（　　）
A．[$\sqrt{3}$，+∞）B．（0，$\sqrt{3}$]C．（$\frac{1}{2}$，$\sqrt{3}$]D．（0，$\frac{\sqrt{3}}{2}$]
2．已知函数f（x）=sin（ωx+φ）（ω＞0）的图象如图所示，则f（4）=$\frac{\sqrt{2}}{2}$．
19．已知集合M={x|x＜1}，N={x|x（x-1）＜0}，则M∪N=（　　）
A．∅B．{x|0＜x＜1}C．{x|x＜0}D．{x|x＜1}
18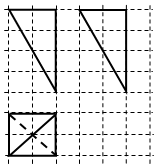．如图是某几何体的三视图，图中方格的单位长度为1，则该几何体外接球的直径为（　　）
A．$2\sqrt{2}$B．$2\sqrt{3}$C．$2\sqrt{6}$D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网