题目内容
13.设x,y满足约束条件$\left\{\begin{array}{l}{2x+y-5≤0}\\{x-y-1≤0}\\{x≥1}\end{array}\right.$,若z=ax+y仅在点(2,1)处取得最大值,则a的取值范围是( )| A. | (-∞,-1) | B. | (2,+∞) | C. | (0,2) | D. | (-1,+∞) |
分析 作出不等式组对应的平面区域,利用z的几何意义,即可得到结论.
解答 解:作出不等式组对应的平面区域如图:
由$\left\{\begin{array}{l}{2x+y-5=0}\\{x-y-1=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$,即A(2,1),
若z=ax+y仅在点(2,1)处取得最大值,
即A是函数取得最大值的最优解,
由z=ax+y得y=-ax+z,
即目标函数的斜率k=-a,
要使是函数取得最大值的最优解,
若a=0,y=z,不满足条件,
若-a>0,此时直线在B处取得最大值,不满足条件.
若-a<0,即a>0时,则满足-a<-2,即a>2,
故选:B.
点评 本题主要考查线性规划的应用,利用z的几何意义,通过数形结合是解决本题的关键.注意对直线斜率进行分类讨论.

练习册系列答案
相关题目
4.要得到函数y=sin(2x+$\frac{π}{3}$)的图象,只需将函数y=cos2x的图象( )
| A. | 向左平移$\frac{π}{12}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向右平移$\frac{π}{12}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
8.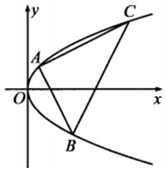 已知A、B、C是抛物线y2=2px(p>0)上三个不同的点,且AB⊥AC.
已知A、B、C是抛物线y2=2px(p>0)上三个不同的点,且AB⊥AC.
(Ⅰ)若A(1,2),B(4,-4),求点C的坐标;
(Ⅱ)若抛物线上存在点D,使得线段AD总被直线BC平分,求点A的坐标.
 已知A、B、C是抛物线y2=2px(p>0)上三个不同的点,且AB⊥AC.
已知A、B、C是抛物线y2=2px(p>0)上三个不同的点,且AB⊥AC.(Ⅰ)若A(1,2),B(4,-4),求点C的坐标;
(Ⅱ)若抛物线上存在点D,使得线段AD总被直线BC平分,求点A的坐标.
18.在2016年高考结束后,针对高考成绩是否达到了考生自己预期水平的情况,某校在高三部分毕业生内部进行了抽样调查,现从高三年级A、B、C、D、E、F六个班随机抽取了50人,将统计结果制成了如下的表格:
(Ⅰ)根据上述的表格,估计该校高三学生2016年的高考成绩达到自己的预期水平的概率;
(Ⅱ)若从E班、F班的抽取对象中,进一步各班随机选取2名同学进行详细调查,记选取的4人中,高考成绩没有达到预期水平的人数为ξ,求随机变量ξ的分布列和数学期望.
| 班级 | A | B | C | D | E | F |
| 抽取人数 | 6 | 10 | 12 | 12 | 6 | 4 |
| 其中达到预期水平的人数 | 3 | 6 | 6 | 6 | 4 | 3 |
(Ⅱ)若从E班、F班的抽取对象中,进一步各班随机选取2名同学进行详细调查,记选取的4人中,高考成绩没有达到预期水平的人数为ξ,求随机变量ξ的分布列和数学期望.
1.某班主任对全班40名学生进行了作业量多少的调查.数据如下表:
(Ⅰ)请完善上表中所缺的有关数据;
(Ⅱ)根据表中数据,问是否有95%的把握认为“喜欢玩游戏与作业量的多少有关系”?
附:χ2=$\frac{{n{{(n}_{11}n}_{22}{{-n}_{12}n}_{21})}^{2}}{{(n}_{11}{+n}_{12}){(n}_{21}{+n}_{22}){(n}_{11}{+n}_{21}){(n}_{12}{+n}_{22})}$.
| 认为作业多 | 认为作业不多 | 总计 | |
| 喜欢玩游戏 | 20 | 10 | |
| 不喜欢玩游戏 | 2 | 8 | |
| 总计 |
(Ⅱ)根据表中数据,问是否有95%的把握认为“喜欢玩游戏与作业量的多少有关系”?
| P(x2≥k) | 0.100 0.050 0.010 |
| k | 2.706 3.841 6.635 |