题目内容
14.已知函数f(x)为定义域在R上的奇函数,当x>0,f(x)=lnx-2x-f(1),则当x<0时,f(x)的表达式为( )| A. | f(x)=ln(-x)+2x+1 | B. | f(x)=-ln(-x)-2x+1 | C. | f(x)=-ln(-x)-2x-1 | D. | f(x)=-ln(-x)+2x-1 |
分析 求出f(1)的值,设x<0,则-x>0,故f(-x)=ln(-x)-2(-x)+1=-f(x),由此可得函数f(x)的解析式.
解答 解:f(1)=-2-f(1),解得:f(1)=-1,
由奇函数的性质可得:
设x<0,则-x>0,故f(-x)=ln(-x)-2(-x)+1=-f(x),
求得f(x)=-ln(-x)-2x-1,
故选:C.
点评 本题考查了函数的奇偶性问题,考查求函数的解析式问题,是一道基础题.

练习册系列答案
相关题目
6.设集合A={-2,-1,1,2},B={-3,-1,0,2},则A∩B的元素的个数为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 1 |
3.设复数z=-2+i(i为虚数单位),则复数$z+\frac{1}{z}$的虚部为( )
| A. | $\frac{4}{5}$ | B. | $\frac{4}{5}i$ | C. | $\frac{6}{5}$ | D. | $\frac{6}{5}i$ |
2.设向量$\overrightarrow a$,$\overrightarrow b$不平行,向量$λ\overrightarrow a+\overrightarrow b$与$\overrightarrow a+2\overrightarrow b$平行,则实数λ等于( )
| A. | 2 | B. | 4 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
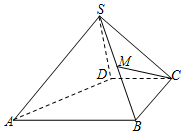 如图,四棱锥S-ABCD中,M是SB的中点,AB∥CD,BC⊥CD,SD⊥面SAB,且AB=BC=2CD=2SD.
如图,四棱锥S-ABCD中,M是SB的中点,AB∥CD,BC⊥CD,SD⊥面SAB,且AB=BC=2CD=2SD.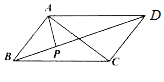
 如图,矩形ABCD的边AB=8,BC=4,以CD为直径在矩形的外部作一半圆,圆心为O,过CD上一点N作AB的垂线交半圆弧于P,交AB于Q,M是曲线PDA上一动点.
如图,矩形ABCD的边AB=8,BC=4,以CD为直径在矩形的外部作一半圆,圆心为O,过CD上一点N作AB的垂线交半圆弧于P,交AB于Q,M是曲线PDA上一动点.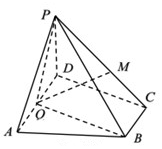 如图在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的一点,PA=PD=4=AD=2BC,CD=2.
如图在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的一点,PA=PD=4=AD=2BC,CD=2.