11. 某公司为了准确地把握市场,做好产品生产计划,对过去四年的数据进行整理得到了第x年与年销量y(单位:万件)之间的关系如表:
某公司为了准确地把握市场,做好产品生产计划,对过去四年的数据进行整理得到了第x年与年销量y(单位:万件)之间的关系如表:
(Ⅰ)在图中画出表中数据的散点图;
(Ⅱ)根据(Ⅰ)中的散点图拟合y与x的回归模型,并用相关系数加以说明;
(Ⅲ)建立y关于x的回归方程,预测第5年的销售量约为多少?.
附注:参考数据:$\sqrt{\sum_{i=1}^4{{{({y_i}-\overline y)}^2}}}≈32.6$,$\sqrt{5}≈2.24$,$\sum_{i=1}^4{{x_i}{y_i}=418}$.
参考公式:相关系数$r=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sqrt{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}\sum_{i=1}^n{{{({y_i}-\overline y)}^2}}}}}$,
回归方程$\widehaty=\widehata+\widehatbx$中斜率和截距的最小二乘法估计公式分别为:$\widehatb=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}$,$\widehata=\overline y-\widehatb\overline x$.
 某公司为了准确地把握市场,做好产品生产计划,对过去四年的数据进行整理得到了第x年与年销量y(单位:万件)之间的关系如表:
某公司为了准确地把握市场,做好产品生产计划,对过去四年的数据进行整理得到了第x年与年销量y(单位:万件)之间的关系如表:| x | 1 | 2 | 3 | 4 |
| y | 12 | 28 | 42 | 56 |
(Ⅱ)根据(Ⅰ)中的散点图拟合y与x的回归模型,并用相关系数加以说明;
(Ⅲ)建立y关于x的回归方程,预测第5年的销售量约为多少?.
附注:参考数据:$\sqrt{\sum_{i=1}^4{{{({y_i}-\overline y)}^2}}}≈32.6$,$\sqrt{5}≈2.24$,$\sum_{i=1}^4{{x_i}{y_i}=418}$.
参考公式:相关系数$r=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sqrt{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}\sum_{i=1}^n{{{({y_i}-\overline y)}^2}}}}}$,
回归方程$\widehaty=\widehata+\widehatbx$中斜率和截距的最小二乘法估计公式分别为:$\widehatb=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}$,$\widehata=\overline y-\widehatb\overline x$.
9.若函数f(x)=2sinωx(0<ω<1)在区间$[{0,\frac{π}{3}}]$上的最大值为1,则ω=( )
0 239809 239817 239823 239827 239833 239835 239839 239845 239847 239853 239859 239863 239865 239869 239875 239877 239883 239887 239889 239893 239895 239899 239901 239903 239904 239905 239907 239908 239909 239911 239913 239917 239919 239923 239925 239929 239935 239937 239943 239947 239949 239953 239959 239965 239967 239973 239977 239979 239985 239989 239995 240003 266669
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
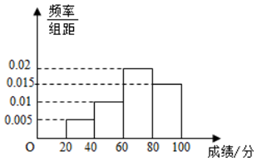 随着社会的发展,食品安全问题渐渐成为社会关注的热点,为了提高学生的食品安全意识,某学校组织全校学生参加食品安全知识竞赛,成绩的频率分布直方图如图所示,数据的分组依次为[20,40),[40,60),[60,80),[80,100),若该校的学生总人数为3000,则成绩不超过60分的学生人数大约为900.
随着社会的发展,食品安全问题渐渐成为社会关注的热点,为了提高学生的食品安全意识,某学校组织全校学生参加食品安全知识竞赛,成绩的频率分布直方图如图所示,数据的分组依次为[20,40),[40,60),[60,80),[80,100),若该校的学生总人数为3000,则成绩不超过60分的学生人数大约为900.