题目内容
14．在区间（0，5）内任取一个实数m，则满足3＜m＜4的概率为$\frac{1}{5}$．分析 直接利用区间测度比得答案．
解答 解：区间（0，5）的区间长度为5．
满足3＜m＜4的区间长度为1．
由测度比为长度比可得满足3＜m＜4的概率P=$\frac{1}{5}$．
故答案为：$\frac{1}{5}$．
点评 本题考查几何概型，明确测度比为测度比是关键，是基础题．
练习册系列答案
相关题目
2．
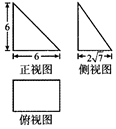《九章算术》是我国古代内容极为丰富的数学名著，系统地总结了战国、秦、汉时期的数学成就．书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”，若某“阳马”的三视图如图所示（单位：cm），则该阳马的外接球的表面积为（ ）
《九章算术》是我国古代内容极为丰富的数学名著，系统地总结了战国、秦、汉时期的数学成就．书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”，若某“阳马”的三视图如图所示（单位：cm），则该阳马的外接球的表面积为（ ）| A． | 100π cm2 | B． | $\frac{500π}{3}$ cm2 | C． | 400π cm2 | D． | $\frac{4000π}{3}$ cm2 |
9．若函数f（x）=2sinωx（0＜ω＜1）在区间$[{0，\frac{π}{3}}]$上的最大值为1，则ω=（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
19．已知集合A={x∈R|0＜x≤5}，B={x∈R|log2x＜2}，则（∁AB）∩Z=（ ）
| A． | {4} | B． | {5} | C． | [4，5] | D． | {4，5} |
11．函数y=（x+1）3当x=-1时（ ）
| A． | 有极大值 | B． | 有极小值 | ||
| C． | 既无极大值，也无极小值 | D． | 无法判断 |