��Ŀ����
8���ס������˽���Χ�������Լ������ʤ������ֱ��Ӯ�ñ�����������$\frac{2}{3}$����δ������ʤ�����ж���ʤ��������Ӯ�ñ���������ÿ�ּ�ʤ�ĸ���Ϊ$\frac{2}{3}$���һ�ʤ�ĸ���Ϊ$\frac{1}{3}$�����ֱ����������������������4�����ڣ��� 4 �֣�Ӯ�ñ����ĸ��ʣ�
���� X Ϊ��������ʤ��ʱ���ܾ�������X�ķֲ��к���ѧ������
���� �����ݸ��ʵij˷���ʽ�������Ӧ�ĸ��ʣ����ɵõ����ۣ�
����������ɢ����������ֱ������Ӧ�ĸ��ʣ�������X�ķֲ��У��Լ���ѧ������
��� �⣺��I����A��ʾ����4�����ڣ���4�֣�Ӯ�ñ��������¼���Ak��ʾ��k�ּ�ʤ��Bk��ʾ��k���һ�ʤ��
��P��Ak��=$\frac{2}{3}$��P��Bk��=$\frac{1}{3}$��k=1��2��3��4��5
P��A��=P��A1A2��+P��B1A2A3��+P��A1B2A3A4��=��$\frac{2}{3}$��2+$\frac{1}{3}��$��$\frac{2}{3}$��2+$\frac{2}{3}$��$\frac{1}{3}$����$\frac{2}{3}$��2=$\frac{56}{81}$��
����X�Ŀ���ȡֵΪ2��3��4��5��
P��X=2��=P��A1A2��+P��B1B2��=$\frac{5}{9}$��
P��X=3��=P��B1A2A3��+P��A1B2B3��=$\frac{2}{9}$��
P��X=4��=P��A1B2A3A4��+P��B1A2B3B4��=$\frac{10}{81}$��
P��X=5��=P��A1B2A3B4A5��+P��B1A2B3A4B5��+P��B1A2B3A4A5��+P��A1B2A3B4B5��=$\frac{8}{81}$��
����P��X=5��=1-P��X=2��-P��X=3��-P��X=4��=$\frac{8}{81}$��
�ʷֲ���Ϊ��
| X | 2 | 3 | 4 | 5 |
| P | $\frac{5}{9}$ | $\frac{2}{9}$ | $\frac{10}{81}$ | $\frac{8}{81}$ |
���� ���⿼����������¼��������¼��ĸ��ʼ��㹫ʽ����������ķֲ�������ѧ������������������������������������е��⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| A�� | $3\sqrt{3}$ | B�� | $2\sqrt{6}$ | C�� | $\sqrt{21}$ | D�� | $2\sqrt{5}$ |
��1
| ͣ������d���ף� | ��10��20] | ��20��30] | ��30��40] | ��40��50] | ��50��60] |
| Ƶ�� | 26 | a | b | 8 | 2 |
| ƽ��ÿ����ѪҺ�ƾ�����x���� | 10 | 30 | 50 | 70 | 90 |
| ƽ��ͣ������y�� | 30 | 50 | 60 | 70 | 90 |
������a��b��ֵ�������Ƽ�ʻԱ��״̬��ͣ�������ƽ������
��������С���˷����ɱ�2�����ݼ���y����x�Ļع鷽��$\hat y=\hat bx+\hat a$��
���ò����Ŷ���Ϊ����ʻԱ�ƺ�ݳ���ƽ����ͣ�����롱y���ڣ�������״̬�µ�ͣ������ƽ������3�������϶���ʻԱ�ǡ����ݡ�������ݣ����еĻع鷽�̣�Ԥ�ÿ����ѪҺ�ƾ��������ڶ��ٺ���ʱΪ�����ݡ���
����������һ�����ݣ�x1��y1������x2��y2����������xn��yn������ع�ֱ��$\hat y=\hat bx+\hat a$��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\bar x\bar y}}{{\sum_{i=1}^n{x_i^2}-n{{\bar x}^2}}}$��$\hat a=\bar y-\hat b\bar x$����
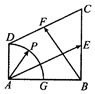 ��ֱ������ABCD�У�AB��AD��AD��BC��AB=BC=2AD=2��E��F�ֱ�ΪBC��CD���е㣬��AΪԲ�ģ�ADΪ�뾶��Բ��AB��G����P��$\widehat{DG}$���˶�����ͼ������$\overrightarrow{AP}$=��$\overrightarrow{AE}$+��$\overrightarrow{BF}$�����Цˣ��̡�R����6��+�̵�ȡֵ��Χ�ǣ�������
��ֱ������ABCD�У�AB��AD��AD��BC��AB=BC=2AD=2��E��F�ֱ�ΪBC��CD���е㣬��AΪԲ�ģ�ADΪ�뾶��Բ��AB��G����P��$\widehat{DG}$���˶�����ͼ������$\overrightarrow{AP}$=��$\overrightarrow{AE}$+��$\overrightarrow{BF}$�����Цˣ��̡�R����6��+�̵�ȡֵ��Χ�ǣ�������| A�� | [1��$\sqrt{2}$] | B�� | [$\sqrt{2}$��2$\sqrt{2}$] | C�� | [2��2$\sqrt{2}$] | D�� | [1��2$\sqrt{2}$] |
| A�� | ��-�ޣ�e�� | B�� | ��1��+�ޣ� | C�� | ��1��e�� | D�� | ��e��+�ޣ� |
| A�� | 3 | B�� | 4 | C�� | 2 | D�� | 5 |
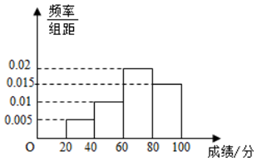 �������ķ�չ��ʳƷ��ȫ���⽥����Ϊ����ע���ȵ㣬Ϊ�����ѧ����ʳƷ��ȫ��ʶ��ijѧУ��֯ȫУѧ���μ�ʳƷ��ȫ֪ʶ�������ɼ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ�����ݵķ�������Ϊ[20��40����[40��60����[60��80����[80��100��������У��ѧ��������Ϊ3000����ɼ�������60�ֵ�ѧ��������ԼΪ900��
�������ķ�չ��ʳƷ��ȫ���⽥����Ϊ����ע���ȵ㣬Ϊ�����ѧ����ʳƷ��ȫ��ʶ��ijѧУ��֯ȫУѧ���μ�ʳƷ��ȫ֪ʶ�������ɼ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ�����ݵķ�������Ϊ[20��40����[40��60����[60��80����[80��100��������У��ѧ��������Ϊ3000����ɼ�������60�ֵ�ѧ��������ԼΪ900��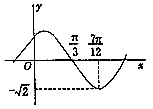 ��1����f��x��=tan��3x-$\frac{��}{4}$���Ķ�����
��1����f��x��=tan��3x-$\frac{��}{4}$���Ķ�����