17.已知公差不为零的等差数列{an}中,a2=4,且a1,a3,a9成等比数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=an+2${\;}^{{a}_{n}}$,求数列{bn}的前n项和Tn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=an+2${\;}^{{a}_{n}}$,求数列{bn}的前n项和Tn.
15.若m,n是两条不同的直线,α是一个平面,则下列说法正确的是( )
| A. | 若m∥α,n∥α,则m∥n | B. | 若m⊥α,n⊥α,则m∥n | C. | 若m⊥n,n?α,则m⊥α | D. | 若m∥n,m∥α,则n∥α |
14.已知函数f(x)=2x+sinx,不等式f(m2)+f(2m-3)<0(其中m∈R)的解集是( )
| A. | (-3,1) | B. | (-1,3) | C. | (-∞,-3)∪(1,+∞) | D. | (-∞,-1)∪(3,+∞) |
13.设直角坐标平面内与两个定点A(-2,0),B(2,0)的距离之差的绝对值等于2的点的轨迹是E.过点B作与x轴垂直的直线l与曲线E交于C,D两点,则$\overrightarrow{AC}•\overrightarrow{BD}$=( )
| A. | -9 | B. | -3 | C. | 3 | D. | 9 |
12.已知ω为正整数,若函数f(x)=sinωx+cosωx在区间(-$\frac{π}{3}$,$\frac{π}{6}$)内单调递增,则函数f(x)最小正周期为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
11.已知α为锐角,若cos(α+$\frac{π}{4}$)=$\frac{5}{13}$,则sinα=( )
| A. | $\frac{5\sqrt{2}}{13}$ | B. | $\frac{12}{13}$ | C. | $\frac{7\sqrt{2}}{26}$ | D. | $\frac{17\sqrt{2}26}{\;}$ |
10.已知复数z满足(2+i)z=2-i(i为虚数单位),则z=( )
| A. | 3+4i | B. | 3-4i | C. | $\frac{3}{5}$+$\frac{4}{5}$i | D. | $\frac{3}{5}$-$\frac{4}{5}$i |
9.已知集合A={x|x2-8x+12≤0},B={x|x≥5},则A∩(∁RB)=( )
0 239788 239796 239802 239806 239812 239814 239818 239824 239826 239832 239838 239842 239844 239848 239854 239856 239862 239866 239868 239872 239874 239878 239880 239882 239883 239884 239886 239887 239888 239890 239892 239896 239898 239902 239904 239908 239914 239916 239922 239926 239928 239932 239938 239944 239946 239952 239956 239958 239964 239968 239974 239982 266669
| A. | [5,6] | B. | [2,5] | C. | [2,5) | D. | (-∞,5) |
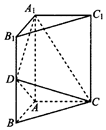 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=$\frac{1}{2}$AA1=a,AB⊥AC,D是棱BB1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=$\frac{1}{2}$AA1=a,AB⊥AC,D是棱BB1的中点.