题目内容
18.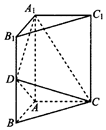 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=$\frac{1}{2}$AA1=a,AB⊥AC,D是棱BB1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=$\frac{1}{2}$AA1=a,AB⊥AC,D是棱BB1的中点.(Ⅰ)证明:平面A1DC⊥平面ADC
(Ⅱ)求平面A1DC将此三棱柱分成的两部分的体积之比.
分析 (Ⅰ)推导出AA1⊥AC,AB⊥AC,从而AC⊥平面ABB1A1,进而AC⊥A1D,再求出AB⊥AC,AD⊥A1D,由此能证明A1D⊥平面ADC.
又∵A1D?平面A1DC,∴平面A1DC⊥平面ADC.
(Ⅱ)平面A1DC将三棱柱分成上、下两部分,其上面部分几何体为四棱锥A-B1C1CD,下面部分几何体为四棱锥C-ABDA1.由此能求出两部分几何体的体积之比.
解答 证明:(Ⅰ)在三棱柱中,有AA1⊥AC,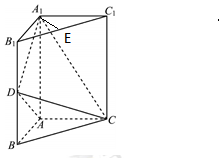
又∵AB⊥AC,AB∩AC=A,
∴AC⊥平面ABB1A1,
∵A1D?平面ABB1A1,∴AC⊥A1D,
由AB=AC=$\frac{1}{2}$AA1=a,AB⊥AC,D是棱BB1的中点.
∴AD=${A}_{1}D=\sqrt{2}a$,AA1=2a,
则$A{D}^{2}+{A}_{1}{D}^{2}$=2a2+2a2=4a2=AA12,∴AD⊥A1D,
∵AD∩AC=A,∴A1D⊥平面ADC.
又∵A1D?平面A1DC,∴平面A1DC⊥平面ADC.
解:(Ⅱ)平面A1DC将三棱柱分成上、下两部分,
其上面部分几何体为四棱锥A-B1C1CD,下面部分几何体为四棱锥C-ABDA1.
在平面A1B1C1中,过点A1作A1E⊥B1C1,垂足为E,
则A1E⊥平面B1C1CD,
∴A1E是四棱锥A1-B1C1CD的高,
在Rt△A1B1C1中,∵A1B1=A1C1=a,∴${A}_{1}E=\frac{\sqrt{2}}{2}a$.
B1C1CD为直角梯形,其面积${S}_{{B}_{1}{C}_{1}CD}=\frac{1}{2}({B}_{1}D+{C}_{1}C)$•B1C1=$\frac{3\sqrt{2}}{2}{a}^{2}$,
∴四棱锥A1-B1C1CD的体积${V}_{{A}_{1}-{B}_{1}{C}_{1}CD}=\frac{1}{3}{S}_{{B}_{1}{C}_{1}CD}$•A1E=$\frac{1}{2}{a}^{3}$.
∵三棱柱ABC-A1B1C1的体积${V}_{ABC-{A}_{1}{B}_{1}{C}_{1}}$=${S}_{ABC-{A}_{1}{B}_{1}{C}_{1}}$=S△ABC•AA1=$\frac{1}{2}{a}^{2}•2a={a}^{3}$,
所以下部分几何体C-ABDA1的体积${V}_{C-ABCD{A}_{1}}$=${V}_{ABC-{A}_{1}{B}_{1}{C}_{1}}$-${V}_{{A}_{1}-{B}_{1}{C}_{1}CD}$=$\frac{1}{2}{a}^{3}$,
所以两部分几何体的体积之比为1:1.
点评 本题考查平面与平面垂直的证明,考查几何体的两部分的比值的求法,考查空间中线线、线面、面面间的位置关系,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、数形结合思想、函数与方程思想是,是中档题.

| A. | y=±3x | B. | $y=±\frac{1}{2}x$ | C. | y=±2x | D. | $y=±\frac{1}{3}x$ |
| A. | a>1 | B. | a≤-$\frac{3}{4}$ | C. | a≥1或a<-$\frac{3}{4}$ | D. | a>1或a≤-$\frac{3}{4}$ |
| A. | -9 | B. | -3 | C. | 3 | D. | 9 |
| A. | (-2,5] | B. | [-2,5] | C. | (2,5] | D. | [2,5] |
| x | 3 | 4 | 5 | 6 | 7 |
| y | 4.0 | 2.5 | -0.5 | 0.5 | -2.0 |
| A. | 1.4 | B. | -1.4 | C. | 1.2 | D. | -1.2 |