题目内容
10.已知复数z满足(2+i)z=2-i(i为虚数单位),则z=( )| A. | 3+4i | B. | 3-4i | C. | $\frac{3}{5}$+$\frac{4}{5}$i | D. | $\frac{3}{5}$-$\frac{4}{5}$i |
分析 把已知等式变形,再由复数代数形式的乘除运算化简得答案.
解答 解:由(2+i)z=2-i,得$z=\frac{2-i}{2+i}=\frac{(2-i)^{2}}{(2+i)(2-i)}=\frac{3-4i}{5}=\frac{3}{5}-\frac{4}{5}i$,
故选:D.
点评 本题考查复数代数形式的乘除运算,是基础的计算题.

练习册系列答案
相关题目
20.已知实数x,y满足不等式$\left\{\begin{array}{l}x+y≤2\\ 2x+y≤3\\ x≥0\\ y≥0\end{array}\right.$,则3x+2y的最大值为( )
| A. | 0 | B. | 2 | C. | 4 | D. | 5 |
1.已知i是虚数单位,复数z满足$\frac{z}{2+z}=i$,则复数z在复平面内对应的点的坐标是( )
| A. | $(-\frac{1}{2},\frac{1}{2})$ | B. | (-1,1) | C. | $(\frac{1}{2},-\frac{1}{2})$ | D. | (1,-1) |
18.函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的图象与$g(x)=2co{s^2}({x-\frac{π}{6}})+1$的图象的对称轴相同,则f(x)的一个递增区间为( )
| A. | $[{-\frac{5π}{6},\frac{π}{6}}]$ | B. | $[{-\frac{π}{3},\frac{π}{6}}]$ | C. | $[{-\frac{5π}{12},\frac{π}{12}}]$ | D. | $[{\frac{π}{12},\frac{7π}{12}}]$ |
15.若m,n是两条不同的直线,α是一个平面,则下列说法正确的是( )
| A. | 若m∥α,n∥α,则m∥n | B. | 若m⊥α,n⊥α,则m∥n | C. | 若m⊥n,n?α,则m⊥α | D. | 若m∥n,m∥α,则n∥α |
19.已知直线l:y=kx-k与抛物线C:y2=4x及其准线分别交于M,N两点,F为抛物线的焦点,若$2\overrightarrow{FM}=\overrightarrow{MN}$,则实数k等于( )
| A. | $±\frac{{\sqrt{3}}}{3}$ | B. | ±1 | C. | $±\sqrt{3}$ | D. | ±2 |
9.已知点的极坐标为$(2,\frac{2π}{3})$那么它的直角坐标为( )
| A. | $(\sqrt{3},-1)$ | B. | $(-\sqrt{3},-1)$ | C. | $(-1,\sqrt{3})$ | D. | $(-1,-\sqrt{3})$ |
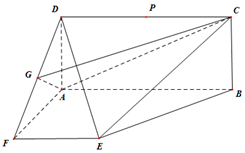 已知矩形ABCD与直角梯形ABEF,∠DAF=∠FAB=90°,点G为DF的中点,AF=EF=$\frac{1}{2}AB=\sqrt{3}$,P在线段CD上运动.
已知矩形ABCD与直角梯形ABEF,∠DAF=∠FAB=90°,点G为DF的中点,AF=EF=$\frac{1}{2}AB=\sqrt{3}$,P在线段CD上运动.