题目内容
17.已知公差不为零的等差数列{an}中,a2=4,且a1,a3,a9成等比数列.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=an+2${\;}^{{a}_{n}}$,求数列{bn}的前n项和Tn.
分析 (I)利用等差数列与等比数列的信托公司即可得出.
(II)l利用等差数列与等比数列的求和公式即可得出.
解答 解:(Ⅰ)设等差数列{an}的公差为d≠0,∵a2=4,且a1,a3,a9成等比数列.
即4-d,4+d,4+7d成等比数列,
所以有(4-d)(4+7d)=(4+d)2,
即d2-2d=0,d≠0.
解得d=2,
∴an=a2+(n-2)×2=4+2n-4=2n.
(Ⅱ)由(Ⅰ)知:bn=an+${2}^{{a}_{n}}$=2n+4n,
∴Tn=2(1+2+…+n)+(4+42+…+4n)
=$2×\frac{n(1+n)}{2}$+$\frac{4({4}^{n}-1)}{4-1}$
=n2+n+$\frac{{4}^{n+1}-4}{3}$.
点评 本题考查了等差数列与等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
7.某位股民购进某只股票,在接下来的交易时间内,他的这只股票先经历了3次涨停(每次上涨10%)又经历了3次跌停(每次下降10%),则该股民这只股票的盈亏情况(不考虑其他费用)为( )
| A. | 略有盈利 | B. | 无法判断盈亏情况 | ||
| C. | 没有盈也没有亏损 | D. | 略有亏损 |
8.如果实数x,y满足约束条件$\left\{\begin{array}{l}{3x+y-6≤0}\\{x-y-2≤0}\\{x≥1}\end{array}\right.$,则z=$\frac{y+1}{x+1}$的最大值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
12.已知ω为正整数,若函数f(x)=sinωx+cosωx在区间(-$\frac{π}{3}$,$\frac{π}{6}$)内单调递增,则函数f(x)最小正周期为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
6.已知z=(m2-1)+mi在复平面内对应的点在第二象限,则实数m的取值范围是( )
| A. | (-1,1) | B. | (-1,0) | C. | (0,1) | D. | (-∞,1) |
16.掷一颗骰子一次,设事件A=“出现奇数点”,事件B=“出现3点或4点”,则事件A,B的关系是( )
| A. | 互斥但不相互独立 | B. | 相互独立但不互斥 | ||
| C. | 互斥且相互独立 | D. | 既不相互独立也不互斥 |
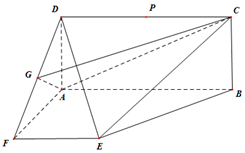 已知矩形ABCD与直角梯形ABEF,∠DAF=∠FAB=90°,点G为DF的中点,AF=EF=$\frac{1}{2}AB=\sqrt{3}$,P在线段CD上运动.
已知矩形ABCD与直角梯形ABEF,∠DAF=∠FAB=90°,点G为DF的中点,AF=EF=$\frac{1}{2}AB=\sqrt{3}$,P在线段CD上运动.