题目内容
12.已知ω为正整数,若函数f(x)=sinωx+cosωx在区间(-$\frac{π}{3}$,$\frac{π}{6}$)内单调递增,则函数f(x)最小正周期为( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
分析 利用辅助角公式将函数f(x)化解,根据x在区间(-$\frac{π}{3}$,$\frac{π}{6}$)内单调递增.建立不等式关系,ω为正整数,即可求出函数f(x)最小正周期.
解答 解:函数f(x)=sinωx+cosωx=$\sqrt{2}$sin(ωx$+\frac{π}{4}$)
x在区间(-$\frac{π}{3}$,$\frac{π}{6}$)内单调递增,
则$\left\{\begin{array}{l}{-\frac{πω}{3}+\frac{π}{4}≥-\frac{π}{2}+2kπ}\\{\frac{πω}{4}+\frac{π}{4}≤\frac{π}{2}+2kπ}\end{array}\right.$,k∈Z,
解得:$\left\{\begin{array}{l}{ω≤\frac{9}{4}-6k}\\{ω≤8k+1}\end{array}\right.$,
∵ω为正整数,
∴ω=1.
那么f(x)═$\sqrt{2}$sin(x$+\frac{π}{4}$)
函数f(x)最小正周期T=$\frac{2π}{1}=2π$.
故选:D.
点评 本题考查了三角函数的性质的运用.属于基础题.

练习册系列答案
相关题目
2.已知椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的一个焦点为F(1,0),离心率为$\frac{{\sqrt{2}}}{2}$,过点F的动直线交M于A,B两点,若x轴上的点P(t,0)使得∠APO=∠BPO总成立(O为坐标原点),则t=( )
| A. | 2 | B. | $\sqrt{2}$ | C. | $-\sqrt{2}$ | D. | -2 |
20.已知集合A={x|2x>1},B={x|x2-5x+6<0},则∁AB( )
| A. | (2,3) | B. | (-∞,2]∪[3,+∞) | C. | (0,2]∪[3,+∞) | D. | [3,+∞) |
17.已知公差不为零的等差数列{an}中,a2=4,且a1,a3,a9成等比数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=an+2${\;}^{{a}_{n}}$,求数列{bn}的前n项和Tn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=an+2${\;}^{{a}_{n}}$,求数列{bn}的前n项和Tn.
4.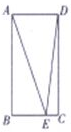 在如图所示的矩形ABCD中,AB=4,AD=2,E为线段BC上的点,则$\overrightarrow{AE}•\overrightarrow{DE}$的最小值为( )
在如图所示的矩形ABCD中,AB=4,AD=2,E为线段BC上的点,则$\overrightarrow{AE}•\overrightarrow{DE}$的最小值为( )
 在如图所示的矩形ABCD中,AB=4,AD=2,E为线段BC上的点,则$\overrightarrow{AE}•\overrightarrow{DE}$的最小值为( )
在如图所示的矩形ABCD中,AB=4,AD=2,E为线段BC上的点,则$\overrightarrow{AE}•\overrightarrow{DE}$的最小值为( )| A. | 12 | B. | 15 | C. | 17 | D. | 16 |
1.函数$f(x)=cos(2x-\frac{2π}{3})+4{cos^2}x-2-\frac{3}{3x-π}(x∈[-\frac{11π}{12},\frac{19π}{12}])$所有零点之和为( )
| A. | $\frac{2π}{3}$ | B. | $\frac{4π}{3}$ | C. | 2π | D. | $\frac{8π}{3}$ |
11.若P(2,1)为圆(x-1)2+y2=25的弦AB的中点,则直线AB的方程为( )
| A. | 2x+y-3=0 | B. | x+y-1=0 | C. | x+y-3=0 | D. | 2x-y-5=0 |
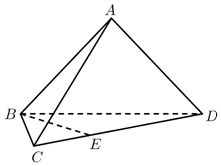 如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,∠CBD=60°,BD=2BC=4,点E在CD上,DE=2EC.
如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,∠CBD=60°,BD=2BC=4,点E在CD上,DE=2EC.