12.已知{an}是公差为2的等差数列,若a1,a3,a4成等比数列,则a2=( )
| A. | -4 | B. | -8 | C. | -10 | D. | -6 |
10.已知某批零件的长度误差(单位:毫米)服从正态分布N(0,32),从中随机取一件,其长度误差落在(3,6)内的概率为( )
附:若随机变量ξ服从正态分布N(μ,σ2),则P(μ-σ<ξ<μ+σ)=0.6826,P(μ-2σ<ξ<μ+2σ)=0.9544.
附:若随机变量ξ服从正态分布N(μ,σ2),则P(μ-σ<ξ<μ+σ)=0.6826,P(μ-2σ<ξ<μ+2σ)=0.9544.
| A. | 0.2718 | B. | 0.0456 | C. | 0.3174 | D. | 0.1359 |
9.执行如图所示的程序框图,输出的a,b的值分别等于( )
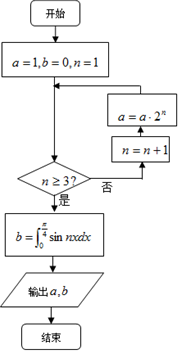

| A. | 32,$-\frac{{\sqrt{2}}}{6}-\frac{1}{3}$ | B. | 32,$\frac{{\sqrt{2}}}{6}+\frac{1}{3}$ | C. | 8,$-\frac{{\sqrt{2}}}{2}-1$ | D. | 32,$\frac{{\sqrt{2}}}{2}+1$ |
8.司机在开机动车时使用手机是违法行为,会存在严重的安全隐患,危及自己和他人的生命.为了研究司机开车时使用手机的情况,交警部门调查了100名机动车司机,得到以下统计:在55名男性司机中,开车时使用手机的有40人,开车时不使用手机的有15人;在45名女性司机中,开车时使用手机的有20人,开车时不使用手机的有25人.
(Ⅰ)完成下面的2×2列联表,并判断是否有99.5%的把握认为开车时使用手机与司机的性别有关;
(Ⅱ)以上述的样本数据来估计总体,现交警部门从道路上行驶的大量机动车中随机抽检3辆,记这3辆车中司机为男性且开车时使用手机的车辆数为X,若每次抽检的结果都相互独立,求X的分布列和数学期望E(X).
参考公式与数据:${Χ^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
0 239770 239778 239784 239788 239794 239796 239800 239806 239808 239814 239820 239824 239826 239830 239836 239838 239844 239848 239850 239854 239856 239860 239862 239864 239865 239866 239868 239869 239870 239872 239874 239878 239880 239884 239886 239890 239896 239898 239904 239908 239910 239914 239920 239926 239928 239934 239938 239940 239946 239950 239956 239964 266669
(Ⅰ)完成下面的2×2列联表,并判断是否有99.5%的把握认为开车时使用手机与司机的性别有关;
| 开车时使用手机 | 开车时不使用手机 | 合计 | |
| 男性司机人数 | |||
| 女性司机人数 | |||
| 合计 |
参考公式与数据:${Χ^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| P(Χ2≥k0) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
