题目内容
8.司机在开机动车时使用手机是违法行为,会存在严重的安全隐患,危及自己和他人的生命.为了研究司机开车时使用手机的情况,交警部门调查了100名机动车司机,得到以下统计:在55名男性司机中,开车时使用手机的有40人,开车时不使用手机的有15人;在45名女性司机中,开车时使用手机的有20人,开车时不使用手机的有25人.(Ⅰ)完成下面的2×2列联表,并判断是否有99.5%的把握认为开车时使用手机与司机的性别有关;
| 开车时使用手机 | 开车时不使用手机 | 合计 | |
| 男性司机人数 | |||
| 女性司机人数 | |||
| 合计 |
参考公式与数据:${Χ^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| P(Χ2≥k0) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (Ⅰ)根据题意填写2×2列联表,计算观测值,对照临界值得出结论;
(Ⅱ)求出任意抽取1辆车中司机为男性且开车时使用手机的概率,
知X的可能取值,且X服从二项分布,计算对应的概率,
写出X的分布列,计算数学期望值.
解答 解:(Ⅰ)填写2×2列联表,如下;
| 开车时使用手机 | 开车时不使用手机 | 合计 | |
| 男性司机人数 | 40 | 15 | 55 |
| 女性司机人数 | 20 | 25 | 45 |
| 合计 | 60 | 40 | 100 |
所以有99.5%的把握认为开车时使用手机与司机的性别有关;
(Ⅱ)由题意,任意抽取1辆车中司机为男性且开车时使用手机的概率是$\frac{40}{100}$=$\frac{2}{5}$,
则X的可能取值为:0,1,2,3,且X~B(3,$\frac{2}{5}$),
可得P(X=k)=${C}_{3}^{k}$•${(1-\frac{2}{5})}^{3-k}$•${(\frac{2}{5})}^{k}$,
所以P(X=0)=${C}_{3}^{0}$•${(\frac{3}{5})}^{3}$•${(\frac{2}{5})}^{0}$=$\frac{27}{125}$,
P(X=1)=${C}_{3}^{1}$•${(\frac{3}{5})}^{2}$•$\frac{2}{5}$=$\frac{54}{125}$,
P(X=2)=${C}_{3}^{2}$•$\frac{3}{5}$•${(\frac{2}{5})}^{2}$=$\frac{36}{125}$,
P(X=3)=${C}_{3}^{3}$•${(\frac{3}{5})}^{0}$•${(\frac{2}{5})}^{3}$=$\frac{8}{125}$;
所以X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{27}{125}$ | $\frac{54}{125}$ | $\frac{36}{125}$ | $\frac{8}{125}$ |
点评 本题考查了二项分布列的性质及其数学期望和独立性检验思想方法,属于中档题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
18.已知(1)正方形的对角线相等;(2)平行四边形的对角线相等;(3)正方形是平行四边形.由(1)、(2)、(3)组合成“三段论”,根据“三段论”推理出一个结论,则这个结论是( )
| A. | 正方形是平行四边形 | B. | 平行四边形的对角线相等 | ||
| C. | 正方形的对角线相等 | D. | 以上均不正确 |
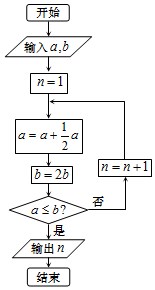 宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若输入的a,b分别为5和2,则输出的n=4.
宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若输入的a,b分别为5和2,则输出的n=4. 某几何体的三视图如图所示(单位:cm),则该几何体的体积V=6cm3,表面积S=16+2$\sqrt{5}$cm2.
某几何体的三视图如图所示(单位:cm),则该几何体的体积V=6cm3,表面积S=16+2$\sqrt{5}$cm2.