题目内容
13.设(3-2x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5,则(a0+a2+a4)2-(a1+a3+a5)2的值为3125(用数字作答)分析 给x赋值1,-1,要求的式子用平方差公式分解,把赋值后的结果代入求出最后结果.
解答 解:因为(3-2x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5,
令x=1得到15=a0+a1+a2+a3+a4+a5,
令x=-1得到55=a0-a1+a2-a3+a4-a5,
又(a0+a2+a4)2-(a1+a3+a5)2=(a0+a1+a2+a3+a4+a5)(a0-a1+a2-a3+a4-a5)=55=3125
故答案为:3125
点评 本题考查二项式定理的应用,本题解题的关键是理解赋值思想,观察要求的式子的结构特点,本题是一个中档题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知△ABC的外心P满足$3\overrightarrow{AP}=\overrightarrow{AB}+\overrightarrow{AC}$,则cosA=( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
4.某几何体的三视图如图所示,则该几何体的表面积是( )
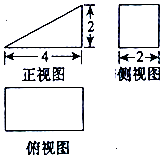

| A. | $20+4\sqrt{5}$ | B. | $12+4\sqrt{5}$ | C. | $20+2\sqrt{5}$ | D. | $12+2\sqrt{5}$ |
8.司机在开机动车时使用手机是违法行为,会存在严重的安全隐患,危及自己和他人的生命.为了研究司机开车时使用手机的情况,交警部门调查了100名机动车司机,得到以下统计:在55名男性司机中,开车时使用手机的有40人,开车时不使用手机的有15人;在45名女性司机中,开车时使用手机的有20人,开车时不使用手机的有25人.
(Ⅰ)完成下面的2×2列联表,并判断是否有99.5%的把握认为开车时使用手机与司机的性别有关;
(Ⅱ)以上述的样本数据来估计总体,现交警部门从道路上行驶的大量机动车中随机抽检3辆,记这3辆车中司机为男性且开车时使用手机的车辆数为X,若每次抽检的结果都相互独立,求X的分布列和数学期望E(X).
参考公式与数据:${Χ^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
(Ⅰ)完成下面的2×2列联表,并判断是否有99.5%的把握认为开车时使用手机与司机的性别有关;
| 开车时使用手机 | 开车时不使用手机 | 合计 | |
| 男性司机人数 | |||
| 女性司机人数 | |||
| 合计 |
参考公式与数据:${Χ^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| P(Χ2≥k0) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
7.为了解某社区居民购买水果和牛奶的年支出费用与购买食品的年支出费用的关系,随机调查了该社区5户家庭,得到如下统计数据表:
根据上表可得回归直线方程$\hat y=\hat bx+\hat a$,其中$\hat b=0.85,\hat a=\overline y-\hat b\overline x$,据此估计,该社区一户购买食品的年支出费用为3.00万元的家庭购买水果和牛奶的年支出费用约为( )
| 购买食品的年支出费用x(万元) | 2.09 | 2.15 | 2.50 | 2.84 | 2.92 |
| 购买水果和牛奶的年支出费用y(万元) | 1.25 | 1.30 | 1.50 | 1.70 | 1.75 |
| A. | 1.79万元 | B. | 2.55万元 | C. | 1.91万元 | D. | 1.94万元 |
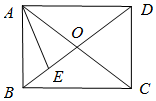 在矩形ABCD中,对角线AC,BD相交于点O,E为BO的中点,若$\overrightarrow{AE}=λ\overrightarrow{AB}+μ\overrightarrow{AD}$(λ,μ为实数),则λμ=$\frac{3}{16}$.
在矩形ABCD中,对角线AC,BD相交于点O,E为BO的中点,若$\overrightarrow{AE}=λ\overrightarrow{AB}+μ\overrightarrow{AD}$(λ,μ为实数),则λμ=$\frac{3}{16}$.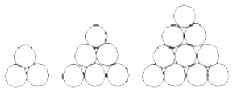 在德国不莱梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第一堆只有一层,就一个乒乓球;第2、3、4、…堆最底层(第一层)分别按图所示方式固定摆放.从第一层开始,每层的小球自然垒放在下一层之上,第n堆第n层就放一个乒乓球,以f(n)表示第n堆的乒乓球总数,则f(3)=10;f(n)=$\frac{1}{6}$n(n+1)(n+2)(答案用n表示).
在德国不莱梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第一堆只有一层,就一个乒乓球;第2、3、4、…堆最底层(第一层)分别按图所示方式固定摆放.从第一层开始,每层的小球自然垒放在下一层之上,第n堆第n层就放一个乒乓球,以f(n)表示第n堆的乒乓球总数,则f(3)=10;f(n)=$\frac{1}{6}$n(n+1)(n+2)(答案用n表示).